Дан ромб со стороной 6 и острым углом 60°. Найдите площадь прямоугольника, вершины которого являются точками касания вписанной окружности со сторонами ромба
математика 8-9 класс
8146
Центр окружности - точка пересечения диагоналей прямоугольника. MP⊥AD, MS⊥BC (AB, BC касательные, ОP, OS - радиусы, проведенные в точку касания).∠SOP=180°-120°=60°. Проведем DH. ∆ADH- прямоугольный. Сумма острых углов равна 90° => ∠ABH=30°. Катет, лежащий против угла в 30 градусов, равен половине гипотенузы => AH=3. По теореме Пифагора DH=3√3. NP=DH=3√3. MS=NP (как диагонали прямоугольника). Площадь прямоугольника равна половине произведения диагоналей на синус угла между ними: S=1/2*3√3*3√3*sin60°=27√3/4
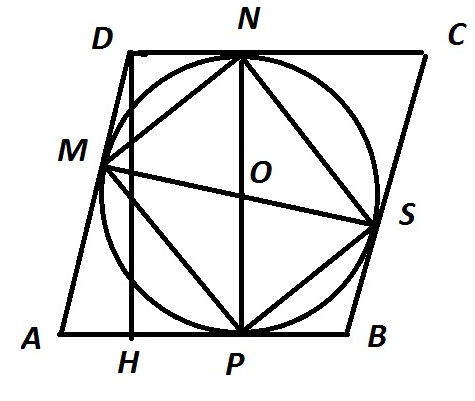
Ответ: 27√3/4

