Задача 74217 доказать последовательность предела (26)...
Условие
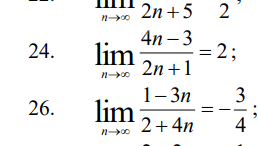
86
Решение
★
Получится:
1) [m]\frac{4n-3}{2n+1} = \frac{4 - 3/n}{2 + 1/n}[/m]
Далее, так как n → oo, то 3/n → 0 и 1/n → 0. Получаем:
[m]\frac{4 - 3/n}{2 + 1/n} = \frac{4 - 0}{2 + 0} = \frac{4}{2} = 2[/m]
2) Точно также
[m]\frac{1-3n}{2+4n} = \frac{1/n - 3}{2/n + 4} = \frac{0 - 3}{0 + 4} = -\frac{3}{4}[/m]
Все решения

