Задача 74193 Спасибо всем. Кто поможет. ...
Условие

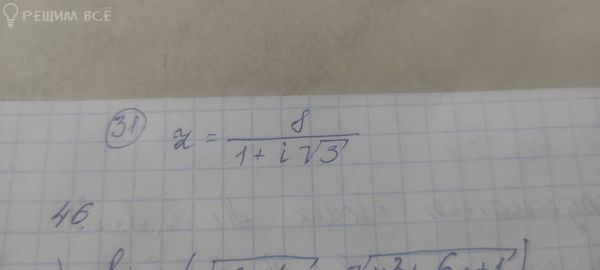
Решение
1. В алгебраической форме:
[m]z = 2(1-i \cdot \sqrt{3}) = 2 - 2\sqrt{3} \cdot i[/m]
В тригонометрической форме:
[m]z = 2 - 2\sqrt{3} \cdot i = 4(\frac{1}{2} - \frac{\sqrt{3}}{2} \cdot i) = 4(cos \frac{5\pi}{3} + i \cdot sin \frac{5\pi}{3})[/m]
В показательной форме:
[m]z = 4(cos \frac{5\pi}{3} + i \cdot sin \frac{5\pi}{3}) = 4e^{i \cdot 5\pi/3}[/m]
2. Найти все корни уравнения w^3 + z = 0
Во-первых, корней будет 3 - по степени уравнения.
Во-вторых, перепишем уравнение так:
w^3 = -z
w^3 = -2 + 2*sqrt(3)*i
[m]w^3 = 4(-\frac{1}{2} + \frac{\sqrt{3}}{2} \cdot i) = 4(cos \frac{2\pi}{3} + i \cdot sin \frac{2\pi}{3})[/m]
Извлекаем кубический корень по формуле Муавра:
[m]w1 = \sqrt[3]{4} \cdot (cos \frac{2\pi/3}{3} + i \cdot sin \frac{2\pi/3}{3})= \sqrt[3]{4} \cdot (cos \frac{2\pi}{9} + i \cdot sin \frac{2\pi}{9}) [/m]
[m]w2 = \sqrt[3]{4} \cdot (cos \frac{2\pi/3+2\pi}{3} + i \cdot sin \frac{2\pi/3+2\pi}{3})= \sqrt[3]{4} \cdot (cos \frac{8\pi}{9} + i \cdot sin \frac{8\pi}{9}) [/m]
[m]w3 = \sqrt[3]{4} \cdot (cos \frac{2\pi/3+4\pi}{3} + i \cdot sin \frac{2\pi/3+4\pi}{3})= \sqrt[3]{4} \cdot (cos \frac{14\pi}{9} + i \cdot sin \frac{14\pi}{9}) [/m]