Задача 74114 Допоможіть, будь ласка. Потрібно на...

63a574f471db7b20f18f0ef7

11/17/2023 6:58:35 AM

Допоможіть, будь ласка. Потрібно на завтра до 19.00

5f3ea7e3faf909182968ddd9

11/17/2023 9:42:12 AM

★

Проводим BF ⊥ AD

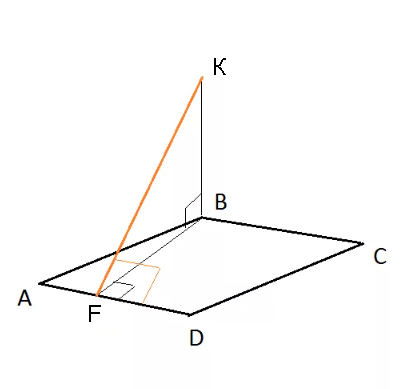
Из прямоугольного треугольника АВF:

BF=AB*sin45 ° =8*sqrt(2)/2=4sqrt(2)

По условию BK ⊥ пл. АВСD ⇒ (KF ⊥ AD по теореме о трех перпендикулярах)

∠ KFB - линейный угол двугранного угла между пл AKD и пл ромба

∠ KFB=60 °

Из прямоугольного треугольника ВKF:

tg∠ KFB=BK/BF ⇒ BK=BF*tg∠ KFB=4sqrt(2) * sqrt(3)=4sqrt(6)

cos∠ KFB=BK/KF ⇒ KF=BF/cos∠ KFB=4sqrt(2)/(sqrt(3)/2)=8sqrt(6)/3


S_( Δ AKD)=(1/2)AD*KF=(1/2)*8*8sqrt(6)/3=32sqrt(6)/3