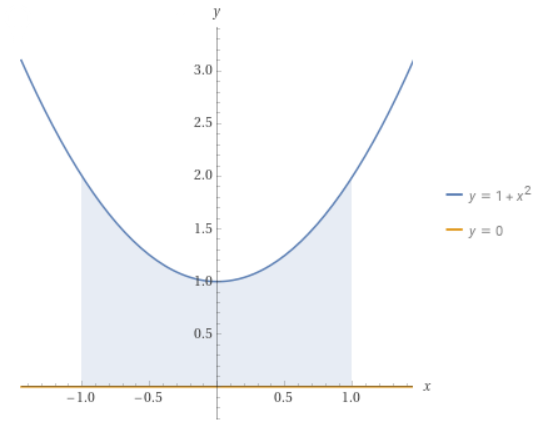
Задача 74066 Вычислить площадь фигуры y=x^2+1, x=-1,...
Условие
y=x^2+1, x=-1, x=1, y=0
????????????
Решение
Функция y = x^2 + 1 - это ветви параболы, которые расположены вверх.
Требуемую площадь можно вычислить как интеграл от функции, ограничивающей область, по заданному диапазону на оси x.
Итак, нам нужно вычислить интеграл следующего вида: S = ∫_(-1,1) (x^2 + 1) dx.
Воспользуемся формулой интеграла от x^n, которая равна (x^(n+1))/(n+1), и добавим также интеграл от 1, который равен x.
Вычислим этот интеграл: S = [(x^3)/3 + x]_(-1, 1).
Подставляем пределы и вычитаем: S = [(1^3)/3 + 1] - [(-1^3)/3 - 1].
Получаем S = [(1/3) + 1] - [(-1/3) - 1].
Финальное вычисление дает S = 8/3.
Ответ: Площадь ограниченной области равна 8/3.