Задача 7399 Дана правильная треугольная призма...
Условие
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC
Решение
1)Рассмотрим ΔАСС1 : уголАСС1 - прямой.
По теореме Пифагора: АС1=sqrt(16 +16) = 4*sqrt(2)
2)Рассмотрим ΔАA1T : уголАA1T - прямой.
По теореме Пифагора: AT=sqrt(16+4) = 2*sqrt(5)
3)Рассмотрим ΔA1TC1 : уголA1TC1 - прямой.
По теореме Пифагора: TC1=sqrt(16-4) = 2*sqrt(3)
4)Рассмотрим ΔАTC1 :
По теореме обратной теореме Пифагора: (АС1)^2 = (AT)^2 + (TC1)^2
32=20+12
32=32
Из этого следует, что ΔАTC1 - прямоугольный (угол АТС1 - прямой).
б)Угол между (АВС) и (АТС1) - это угол между (А1В1С1) и (АТС1);
А1Т ⊥ ТС1 ; АТ ⊥ ТС1 , значит, угол А1ТА - линейный угол двугранного угла между плоскостями(искомый угол)
ΔАА1Т - прямоугольный, угол АА1Т-прямой,
tgАТA1=AA1/A1T=4/2=2
уголАТA1=arctg2.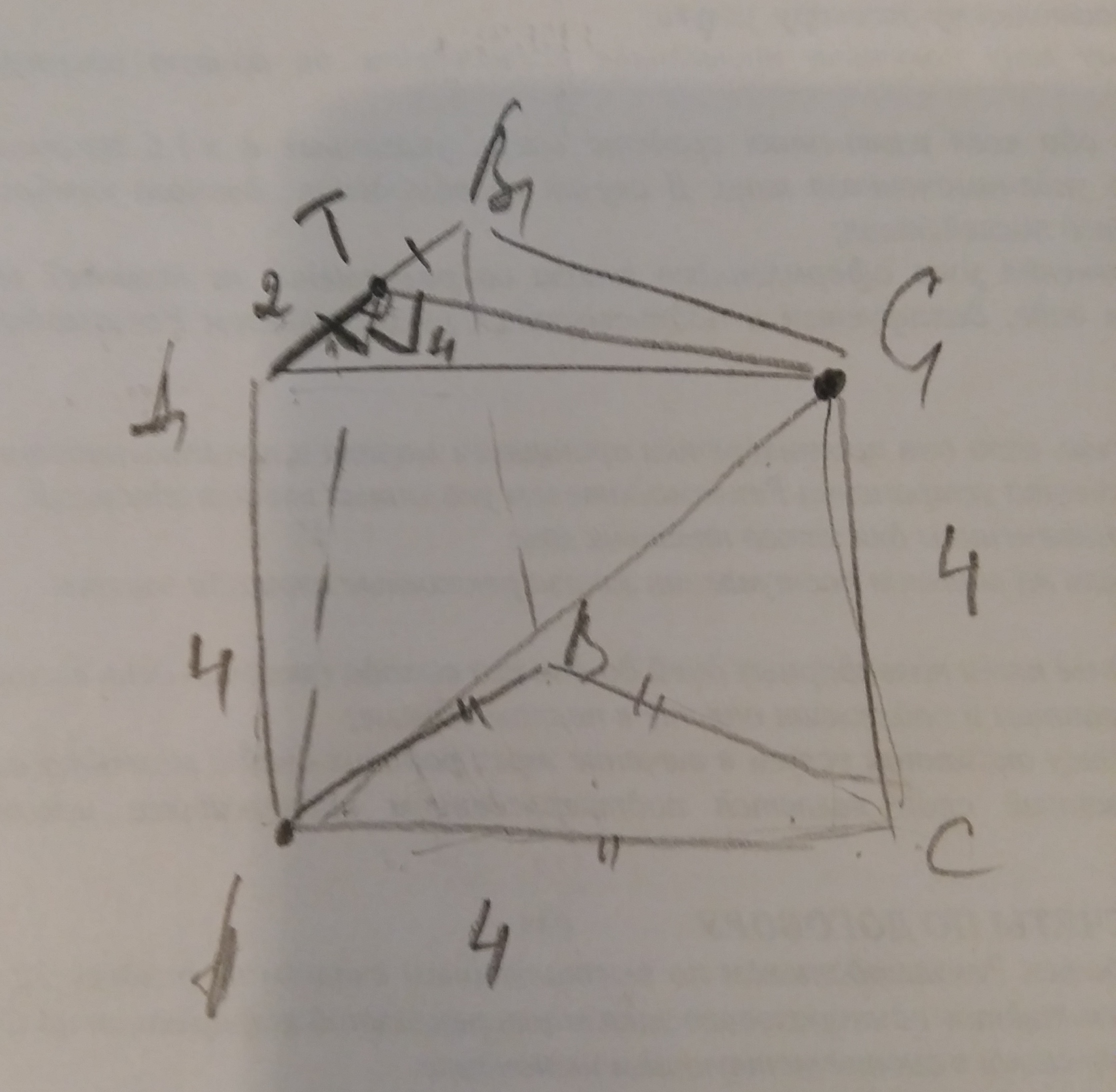
Все решения