Задача 73937 Допоможіть, будь ласка. Потрібно на...
Условие
Решение
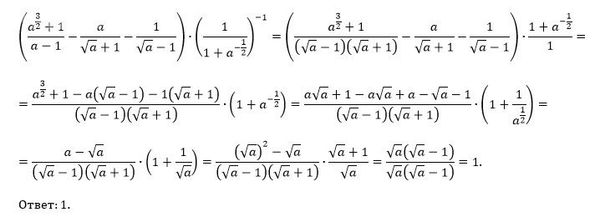
Все решения
[m](\frac{a^{3/2} + 1}{a - 1} - \frac{a}{\sqrt{a} + 1} - \frac{1}{\sqrt{a} - 1}) \cdot (\frac{1}{1 + a^{-1/2}})^{-1} = (\frac{(a^{1/2}+1)(a-a^{1/2}+1)}{(a^{1/2}+1)(a^{1/2}-1)} - \frac{a}{a^{1/2}+1} - \frac{1}{a^{1/2}-1}) \cdot (1 + \frac{1}{a^{1/2}}) = [/m]
[m](\frac{a-a^{1/2}+1}{a^{1/2}-1} - \frac{a}{a^{1/2}+1} - \frac{1}{a^{1/2}-1}) \cdot \frac{a^{1/2}+1}{a^{1/2}} = (\frac{a-a^{1/2}}{a^{1/2}-1} - \frac{a}{a^{1/2}+1}) \cdot \frac{a^{1/2}+1}{a^{1/2}} =[/m]
[m]= (a^{1/2} - \frac{a}{a^{1/2}+1}) \cdot \frac{a^{1/2}+1}{a^{1/2}} = \frac{a+a^{1/2}-a}{a^{1/2}+1} \cdot \frac{a^{1/2}+1}{a^{1/2}} = \frac{a^{1/2}}{a^{1/2}+1} \cdot \frac{a^{1/2}+1}{a^{1/2}} =1[/m]