Задача 73677 Задача 2. Определить размер С, чтобы...
Условие
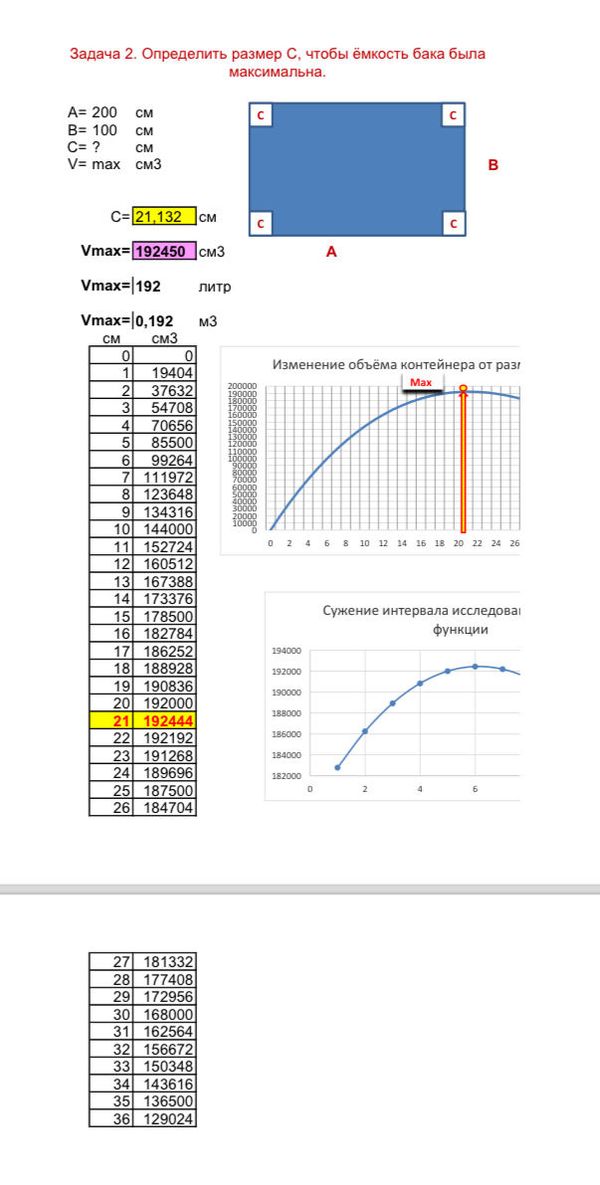
Решение
Я могу рассчитать точное значение С аналитически.
Мы вырезаем квадратики СхС см из прямоугольника 200х100 см.
Получается дно размером (200 - 2С)х(100 - 2С) и высота С.
Объем равен произведению всех трех измерений бака:
V = (200 - 2С)(100 - 2С)*C = 20000C - 600C^2 + 4C^3
Объем будет максимальным, если его производная будет равна 0.
V' = 20000 - 1200C + 12C^2 = 0
3C^2 - 300C + 5000 = 0
D/4 = 150^2 - 3*5000 = 22500 - 15000 = 7500 = (50*sqrt(3))^2
С1 = (150 - 50*sqrt(3))/3 = 50 - 50*sqrt(3)/3 ≈ 21,1325 см
C2 = (150 + 50*sqrt(3))/3 = 50 + 50*sqrt(3)/3 ≈ 78,86 см - не подходит.
С2 не подходит, потому что получается 100 - 2C < 0
Получили: C = 50 - 50*sqrt(3)/3 ≈ 21,1325, тогда объем:
[m]V = (200-2С)(100-2С) \cdot C = (100+\frac{100 \sqrt{3}}{3})(\frac{100 \sqrt{3}}{3})(50-\frac{50 \sqrt{3}}{3}) =[/m]
[m]= \frac{300+100 \sqrt{3}}{3} \cdot \frac{100 \sqrt{3}}{3} \cdot \frac{150-50 \sqrt{3}}{3} = [/m]
Выносим за скобки: 100 в 1-ой и 2-ой дроби и 50 в 3-ей дроби:
[m] =\frac{500000 \sqrt{3}(3+ \sqrt{3})(3- \sqrt{3})}{27} = \frac{500000 \sqrt{3}(9- 3)}{27} =\frac{1000000 \sqrt{3}}{9} ≈ 192450,09[/m]
Ответ: C ≈ 21,1325 см; V ≈ 192450,09