Задача 73604 Допоможіть, будь ласка. Потрібно на...

63a574f471db7b20f18f0ef7

20.10.2023 18:40:42

Допоможіть, будь ласка. Потрібно на завтра до 12.00

5f3eaa23faf909182968dde0

20.10.2023 21:34:32

★

KL – средняя линия ΔАSC, KL || AC и KL=(1/2) AC=6 см.
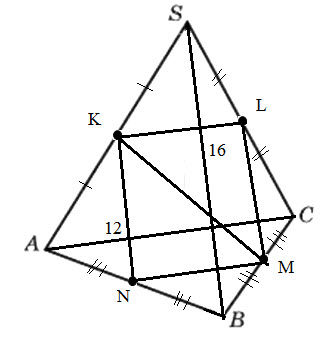
MN – средняя линия ΔАBC, MN || AC и MN=(1/2) AC=6 см.
KN – средняя линия ΔАSB, KN || SB и KN=(1/2) SB=8 см.
ML – средняя линия ΔSBC, ML || SB и ML=(1/2) SB=8 см.
В четырехугольнике KLMN стороны попарно равны и параллельны,
значит, четырехугольник KLMN – прямоугольник.
Тогда ΔKNM прямоугольный, из него по теореме Пифагора находим KM:
KM=sqrt(KN^(2)+MN^(2))=sqrt(6^(2)+8^(2))=sqrt(36+64)=sqrt(100)=10 (см).

Так как ΔАВС равносторонний, то все его стороны равны стороне АС=12 см. Площадь равностороннего треугольника находим по формуле:
S=(a^(2)*sqrt(3))/4=(12^(2)*sqrt(3))/4=36sqrt(3) (см^(2)).