Задача 73472 Дано: t0=4 c, x(t)=5t^2-2t-6. Найти:...
Условие
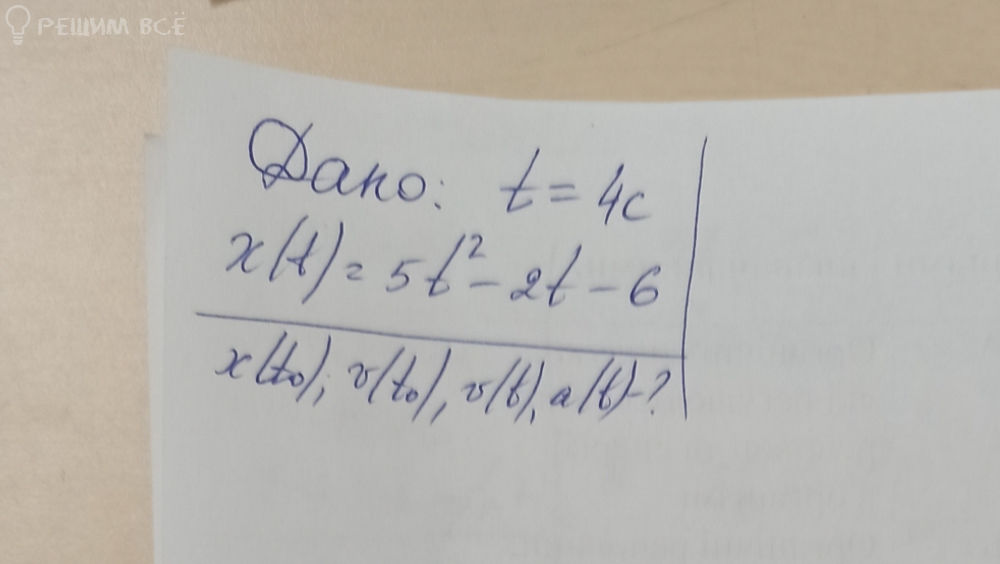
физика колледж
270
Решение
★
t0 = 4 с
x(t) = 5t^2 - 2t - 6
Чтобы найти x(t0), подставим t0 в функцию x(t) :
x(t0) = 5*(4^2) - 2*4 - 6
x(t0) = 5*16 - 8 - 6
x(t0) = 80 - 8 - 6
x(t0) = 66
Теперь найдем скорость, которая является первой производной от x(t).
v(t) = dx(t)/dt = x'(t) = 10t - 2
Найдем v(t0), подставив t0 в функцию v(t):
v(t0) = 10*4 - 2
v(t0) = 40 - 2
v(t0) = 38
Ускорение - это вторая производная от x(t), а значит первая производная от v(t).
a(t) = dv(t)/dt = v'(t) = 10
Так как ускорение является константой, то a(t) = a(t0) = 10.
Итого:
x(t0) = 66
v(t0) = 38
v(t) = 10t - 2
a(t) = 10