Задача 73433 Исследуйте функцию и постройте её...
Условие
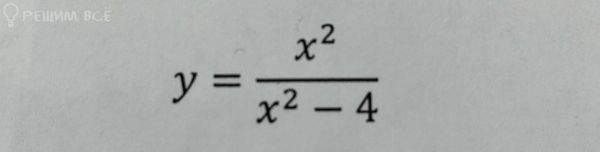
Решение
Область определения (- ∞ ;-2) U (-2;2) U(2;+ ∞ )
2.Точки пересечения с осями.
x=0 ⇒ y=0/((0^2-4)=0
Одна точка (0;0)
3. Исследовать функцию на четность/нечетность.
Функция четная
y(-x)=(-x)^2/((-x)^2-4)=x^2/(x^2-4)=y(x)
4. Найти асимптоты.
[i]Вертикальные [/i]асимптоты
x=-2
x=2
y=1 - [i] горизонтальная[/i] асимптота
5. Найти экстремумы и интервалы монотонности функции.
Находим производную
Применяем правило дифференцирования частного ( дроби):
(u/v)`=(u`*v-u*v`)/v^2
y`= ((x^2)`*(x^2-4)-x^2*(x^2-4)`)/(x^2-4)^2
y`=((2x*(x^2-4)-x^2*(2x))/(x^2-4)^2
y`=2x*(x^2-4-x^2)/(x^2-4)^2
y`=0
x=0
Знак производной:
___+__ (-2) __+__ (0) _-__ (2) __-__
y`>0 на (- ∞ ;-2) и на (2;0 ) , значит функция монотонно возрастает на (- ∞ ;-2) и на (2;0 )
y`<0 на (0; 2) и на (2;+ ∞ ) , значит функция монотонно убывает на (0; 2) и на (2;+ ∞ )
x=0 - точка максимума
f(0)=0
