Задача 73362 При каких a оба корня уравнения x2 - 4ax...
Условие
Решение
y=x^2+4a*x+4-2a+4a^2
является парабола, ветви, которой направлены вверх
Парабола имеет две точки пересечения с осью Ох, если дискриминант квадратного трехчлена положителен
D=(-4a)^2-4*(4-2a+4a^2)=16a^2-16+8a-16a^2=8a-16
D>0
8a-16 >0
[b]a>2[/b]
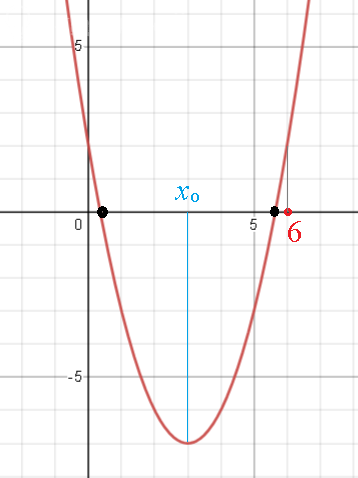
Схематическое расположение графика, оба корня меньше шести на рисунке
Это значит, что вершина параболы тоже меньше шести:
x_(o)=4a/2
2a < 6 ⇒ a<3
И значение функции в вершине отрицательно
f(x_(o))=f(2a)=(2a)^2+4a*(2a)+4-2a+4a^2<0
а значение функции в точке 6 положительно:
f(6)=6^2+4a*6+4-2a+4a^2>0
Все четыре условия в системе
{[b]a>2[/b]
{a<3
{4a^2+22a+40>0
{16a^2-2a+4 <0
Решаем и получаем ответ для параметра a