Задача 73233 ЗДРАВСТВУЙТЕ пожалуйст можете очень...

650179c1521d6e590325a4d4

09.10.2023 20:39:20

ЗДРАВСТВУЙТЕ пожалуйст можете очень срочн помочббб, с графиком и решением прошуу

5f3ea7e3faf909182968ddd9

09.10.2023 21:29:23

★

x^2+y ≤ 3
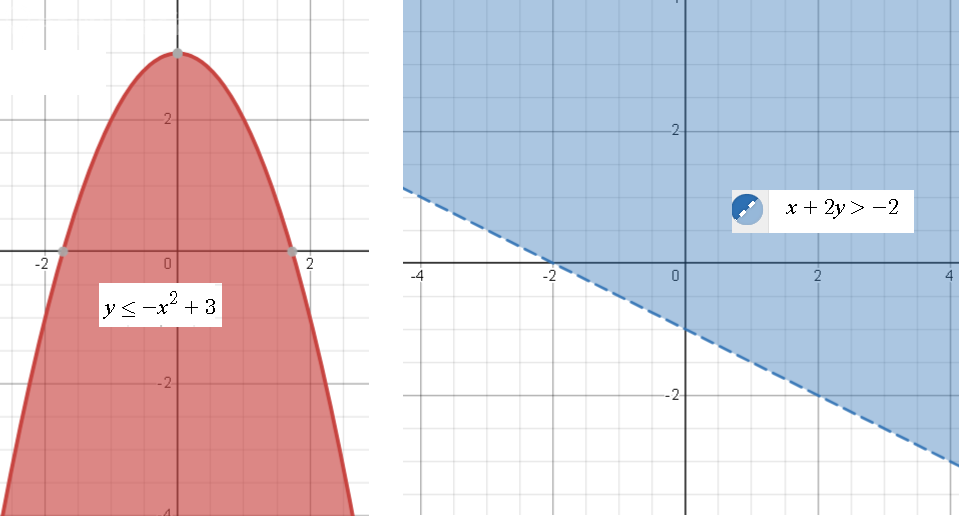
y ≤ -x^2+3
Граница - парабола
y=-x^2+3, ветви вниз.

Парабола разбивает плоскость на две части : внутри параболы и вне параболы

Неравенству удовлетворяет область внутри параболы, закрашенная красным цветом

Как узнать? Взять любую точку , например,(0;-2), которая находится внутри параболы и подставить её координаты

в неравенство:

-2 ≤ -0^2+3 - верно

Значит, неравенству удовлетворяют точки внутри параболы. Эту область и закрашиваем

Если возьмем точку (4;4), которая находится вне параболы и подставить её координаты

в неравенство:

4 ≤ -4^2+3 - неверно

Значит, точки вне параболы не удовлетворяют неравенству.



x+2y>-2
Граница - прямая x+2y=-2

Неравенство строгое, поэтому граница - пунктиром

Прямую строим по точкам:

x=0
2y=-2
y=-1

(0;-1)

x=-2
-2y=0
(-2;0)


Прямая разбивает плоскость на две части. Неравенству удовлетворяет область справа от прямой.

Как узнать? Взять любую точку из этой области, например,(0;0) и подставить её координаты

в неравенство: [m]x +2y>-2 [/m]

[m]30+2\cdot0 ≥-2 [/m] - верно.

Значит область, содержащая точку (0;0) удовлетворяет неравенству,


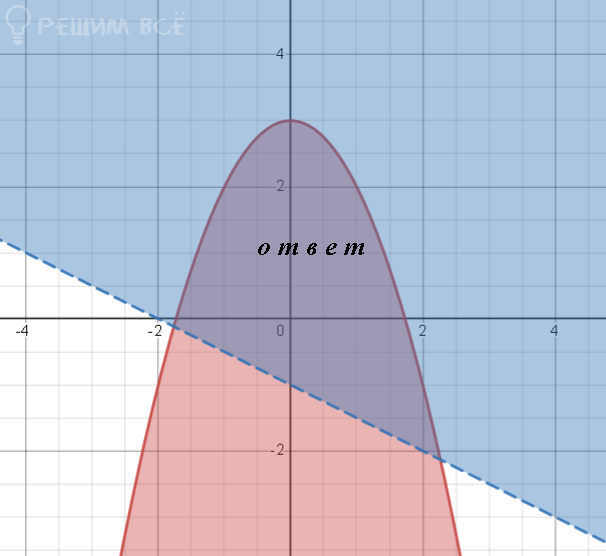
Системе удовлетворяет пересечение областей, см рис. 3
Область сиреневого цвета