Задача 73077 Бревно(стенобитное орудие) массой 125 кг...
Условие
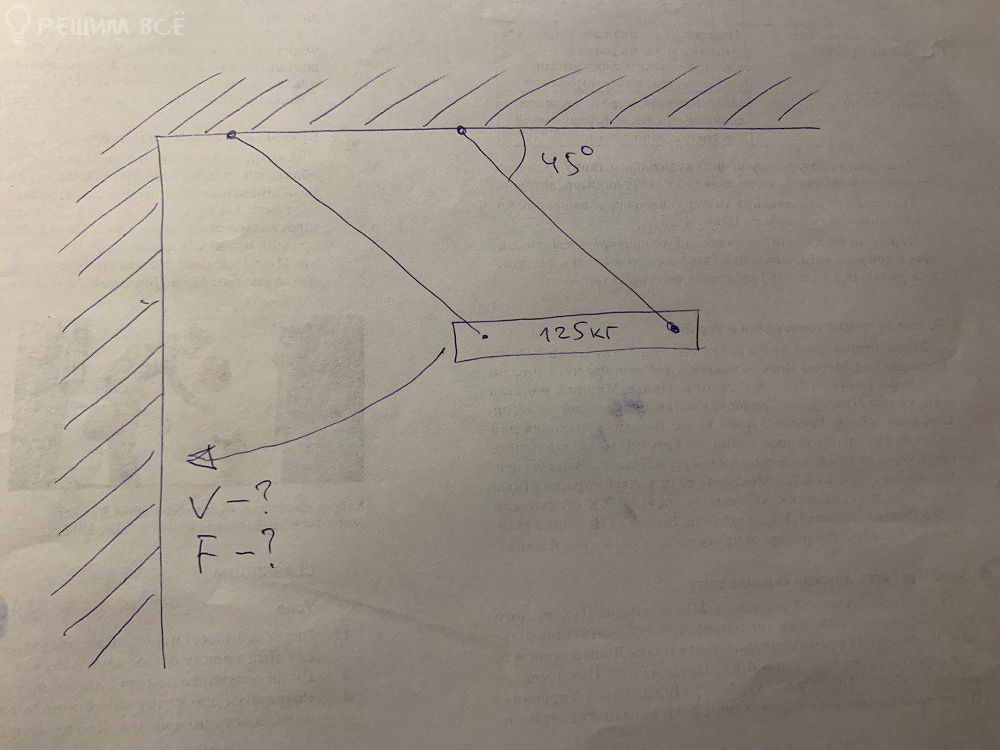
Решение
Для решения этой задачи мы можем использовать законы сохранения энергии. Изначально у бревна есть потенциальная энергия, которая в конечной точке будет превращена в кинетическую энергию.
Найдем потенциальную энергию бревна в его начальном положении:
Потенциальная энергия Eп= масса (m) * ускорение свободного падения (g) * высота (h)
где m = 125 кг, g = 10 м/с², h = 4 м (высота подвешивания,она была найдена геометричемким способом с помощью равнобедренного прямоугольного треугольника.).
Eп = 125 кг * 10 м/с² * 4 м = 5000 Дж .
Затем найдем скорость бревна в нижней точке, используя закон сохранения энергии:
Начальная потенциальная энергия = Кинетическая энергия в нижней точке
Eп = (1/2) * масса * скорость^2
Мы знаем Eп (из шага 1) и массу, и мы ищем скорость:
5000 Дж = (1/2) * 125 кг * скорость^2
Решая уравнение, найдем скорость:
скорость = √((2 * Eп) / масса)
скорость = √((2 * 5000 Дж) / 125 кг) ≈ 10 м/с.
Теперь найдем силу удара в нижней точке, используя второй закон Ньютона (F = m * a), где a - ускорение, равное гравитационному ускорению (g), и скорость бревна (которую мы уже нашли) в данной точке:
F = 125 кг * 10 м/с² ≈ 1250Н