Задача 73024 Вычислите площадь фигуры, ограниченной...
Условие
С РИСУНКОМ!!!
2168
Решение
★
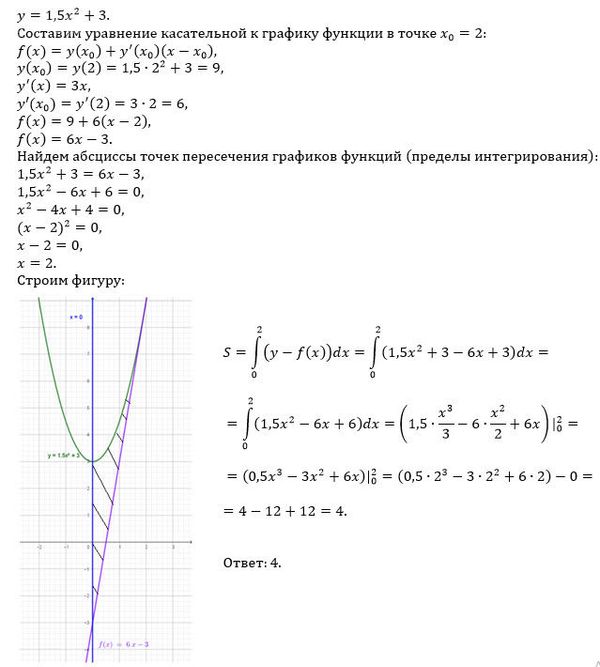
y-y_(o)=f`(x_(o))*(x-x_(o)
f`(x)=(1,5x^2+3)`=1,5*2x=3x
f`(x_(o))=f`(2)=3*2=6
f(x_(o))=1,5*2^2+3=9
y-9=6*(x-2)
[b]y=6x-3[/b]
Касательная y=6x-3 и прямая х=0 ( ось Ох)
пересекаются в точке (0;-3)
Первый предел интегрирования:
x=0
Второй предел интегрирования - точка касания:
x=2
[m]S= ∫^{2} _{0}((1,5x^2+3)-(6x-3))dx=∫^{2} _{0}=(1,5\cdot \frac{x^3}{3}-6\cdot \frac{x^2}{2}+6x)|^{2}_{0}= \frac{2^3}{3}-3\cdot 2:2-6\cdot 2=4[/m]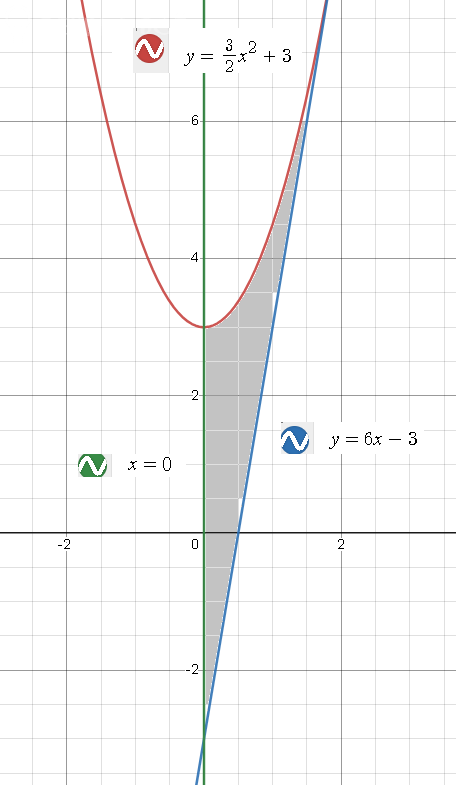
Все решения