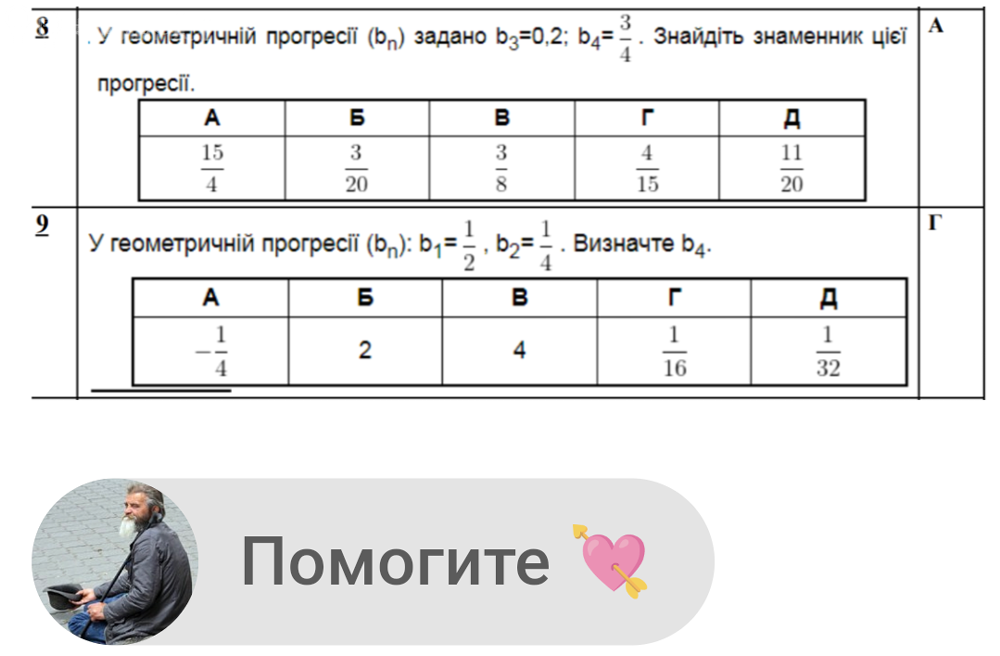
Задача 72656 Номер 9....
Условие
биология 10-11 класс
194
Решение
★
По формуле n-го члена геометрической прогрессии получаем:
b_(n)=b_(1)*q^(n-1).
Найдем знаменатель геометрической прогрессии:
q=b_(2):b_(1)=(1/4):(1/2)=(1/4)*(2/1)=1/2.
Находим b_(4):
b_(4)=(1/2)*(1/2)^(4-1)=(1/2)*(1/2)^(3)=1/16.
Ответ: Г.