Задача 72600 Напишите отве по быстрее ...
Условие
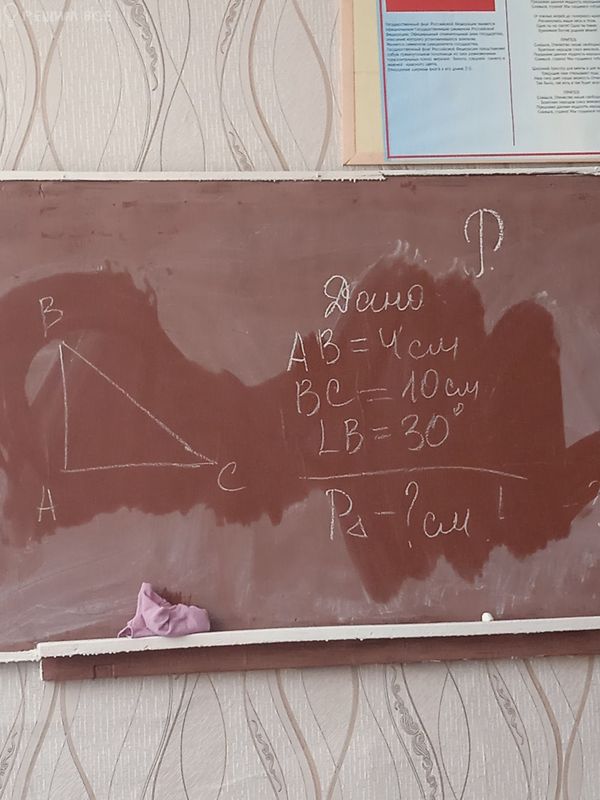
нет в списке 8-9 класс
136
Решение
★
Для решения задачи используем закон синусов, который гласит:
[m]\frac{a}{sin A} = \frac{b}{sin B} = \frac{c}{sin C}[/m],
a, b, c - стороны треугольника. A, B, C - противолежащие углы.
В данном случае, даны стороны AB и BC, а также угол B. Вам необходимо найти периметр треугольника ABC.
1. [m]AC = \frac{AB}{sin B} = \frac{4}{sin 30} = 8 см.[/m]
2. P=4 см+8 см+10 см=22 см
Ответ: 22 см