Задача 72348 Плотность вероятности непрерывной...
Условие
(ответ вводите округлив до двух верных значащих цифр после разделяющей десятичной точки, например, 0.10 вместо 0,1, или 0.28 вместо 0,275, а 0.27 вместо 0,274) 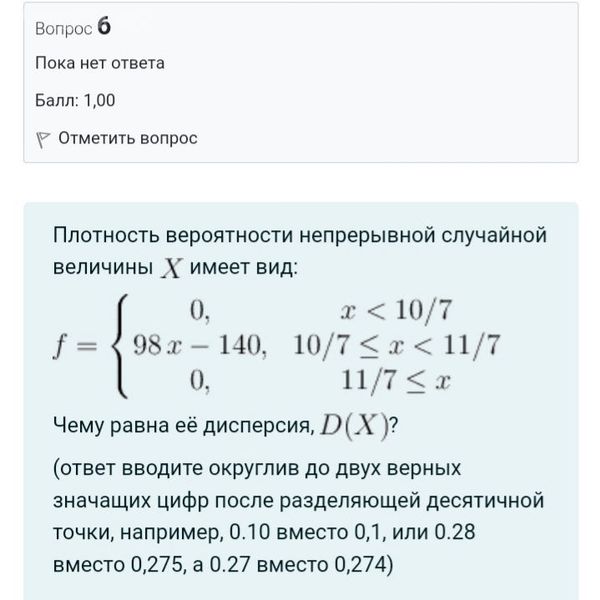
Решение
[m]M(X)=∫ ^{∞ }_{- ∞ }x\cdot f(x)dx[/m]
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
[m]M(X)= ∫ ^{\frac{11}{7}}_{\frac{10}{7}}x\cdot (98x-140)dx=(98\frac{x^3}{3}-70x^2)|^{\frac{11}{7}}_{\frac{10}{7}}=\frac{98}{3}\cdot ((\frac{11}{7})^3-(\frac{10}{7})^3)-70\cdot ((\frac{11}{7})^2-(\frac{10}{7})^2)=[/m]
[m]=\frac{98}{3}\cdot(\frac{11}{7}-\frac{10}{7})\cdot ((\frac{11}{7})^2+\frac{11}{7}\cdot \frac{10}{7}+(\frac{10}{7})^2)-70\cdot (\frac{11}{7}-\frac{10}{7})\cdot (\frac{11}{7}+\frac{10}{7})=[/m]
[m]=\frac{98}{3}\cdot\frac{1}{7}\cdot \frac{121+110+100}{49}+70\cdot \frac{1}{7}\cdot \frac{21}{7}=\frac{32}{21}[/m]
По формуле:
[red]D(X)=M(X^2)-(M(X))^2[/red]
[m]M(X^2)=∫ ^{\frac{11}{7}}_{\frac{10}{7}}x(98x-140)^2dx=∫ ^{\frac{11}{7}}_{\frac{10}{7}}14^2(7x^3-10x^2)^2dx=196∫ ^{\frac{11}{7}}_{\frac{10}{7}}(49x^6-140x^5+10x^4)dx=[/m]
Тогда
[red]D(X)=[/red]