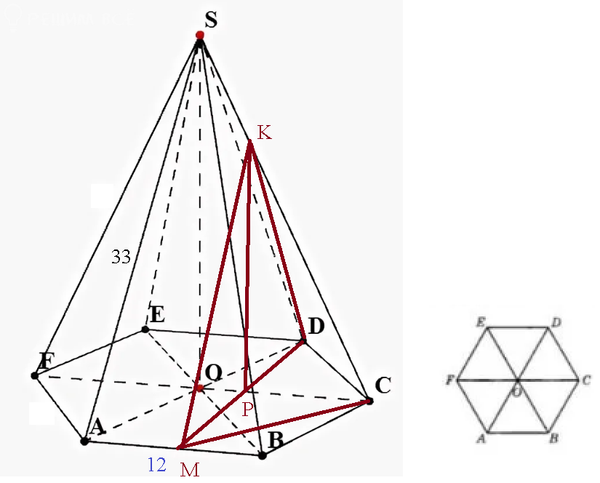
Задача 72331 в правильной шестиугольной пирамиде...

64cf82d60d657664a0bc1cee

06.08.2023 14:25:50

в правильной шестиугольной пирамиде ABCDEF сторона основания AB=12. а боковое ребро SA=33.точка M середина ребра AB. плоскость a перпендикулярна плоскости ABC и содержит точки M и D. прямая SC пересекает плоскость a в точке K
а) докажите, что KM=KD
б) найдите объем пирамиды CDKM

5f3ea7e3faf909182968ddd9

07.08.2023 20:31:13

★

MD ∩ OC=P

PK|| SO ⇒ PK ⊥ ABCDEF ⇒ PK ⊥ MDC

OP || AM

OP - средняя линия Δ ADM ⇒ DP=PM ⇒ [b]a)[/b] Равные проекции имеют равные наклонные ⇒ [b]МК=КD[/b]

ОР=(1/2)AM=3

OC=12
PC=9

SO:PK=OC:PC
PK=(9/12)SO

SO^2=SA^2-AO^2=33^2-12^2=(33-12)*(33+12)=21*45

SO=3sqrt(105)

PK=(3/4)*3sqrt(105)=[b](9/4)sqrt(105)[/b]

Δ PDC

DC=12
PC=9
∠ PCD=60 °

S_(Δ PDC)=(1/2)*12*9*sin60 ° =27sqrt(3)

S(Δ MPC)=S_(Δ PDC)=27sqrt(3)

S_( Δ MDC)=54sqrt(3)


V_(MDCK)=(1/3)S_( Δ MDC)*PK=(1/3)*54sqrt(3)*(9/4)sqrt(105)=[b]45sqrt(35)[/b]