Задача 72220 В треугольнике KLM с периметром 56...
Условие

Решение
Сторона LM на 6 см меньше стороны KM.
LM = KM - 6 = x - 6 см
Сторона KL на 13 см меньше стороны KM.
KL = KM - 13 = x - 13 см
Определение: Периметр - это сумма всех сторон многоугольника.
P = KM + KL + LM = 56 см.
x + (x - 13) + (x - 6) = 56
Раскрываем скобки:
x + x - 13 + x - 6
3x - 19 = 56
3x = 56 - 19
3x = 75
x = 75/3
KM = x = 25 см
LM = KM - 6 = 25 - 6 = 19 см
KL = KM - 13 = 25 - 13 = 12 см
Построить треугольник по трем сторонам, надеюсь, вы сумеете.
2) Пусть у нас треугольник ABC.
Первый угол обозначим A = x.
Этот угол в 3 раза меньше второго угла.
Значит, второй угол B = 3x.
И тот же первый угол на 20° меньше третьего угла.
Значит, третий угол C = x + 20°
Теорема: Сумма углов в треугольнике равна 180°.
x + 3x + x + 20° = 180°
5x + 20° = 180°
5x = 180° - 20°
5x = 160°
x = 160°/5
а) A = x = 32°
B = 3x = 3*32° = 96°
C = x + 20° = 32° + 20° = 52°
б) Так как угол B = 96° > 90°, то треугольник - тупоугольный.
Построить треугольник по 3 углам, надеюсь, тоже сумеете.
3) Теорема: длина каждой стороны треугольника должна быть меньше, чем сумма двух других его сторон.
а) Если стороны относятся, как 3 : 3 : 8, то сумма меньших сторон:
3 + 3 = 6 < 8
Такой треугольник не существует.
б) Если стороны относятся, как 4 : 9 : 9, то сумма меньших сторон:
4 + 9 = 13 > 9
Такой треугольник существует.
Этот треугольник равнобедренный и остроугольный.
Построить его по трем сторонам вы сможете.
в) Углы относятся, как 3 : 5: 7.
Теорема: Сумма углов в треугольнике равна 180°.
Обозначим углы 3x, 5x, 7x.
3x + 5x + 7x = 180°
15x = 180°
x = 180°/15
x = 12°
Углы треугольника:
3x = 3*12° = 36°
5x = 5*12° = 60°
7x = 7*12° = 84°
Этот треугольник разносторонний и остроугольный.
Построить его по трем углам вы тоже сможете.
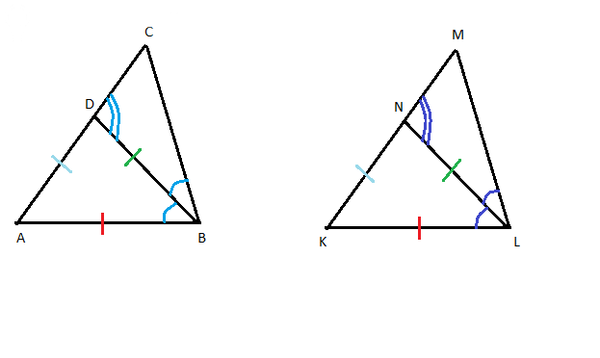
4) Два треугольника показаны на рисунке.
|AB| = |KL| (показаны красной черточкой)
|AD| = |KN| (показаны бирюзовой черточкой)
|BD| = |LN| (показаны зеленой черточкой)
Поэтому треугольник ΔABD = ΔKLN по трем сторонам.
Углы ∠ADB = ∠KNL, тогда ∠CDB = ∠NML (показаны двойными дугами).
Далее, AD и KN - биссектрисы треугольников, значит, углы
∠ABD = ∠CBD (показаны светло-синими одиночными дугами)
∠KLN = ∠MLN (показаны темно-синими одиночными дугами)
Треугольники ΔBCD = ΔMLN по одной стороне (|BD| = |LN|)
и двум углам, прилегающим к этой стороне.
А так как треугольники ΔABD = ΔKLN и ΔBCD = ΔMLN, то
треугольники ΔABC = ΔKLM
Что и требовалось доказать.
5) а) Треугольник ΔEFK равнобедренный, |EF| = |FK|.
Отрезки |OE| = |OF| = |OK| = R - радиусу окружности.
Поэтому треугольники ΔOFE = ΔOFK по трем сторонам.
А значит, и все углы в этих треугольниках равны:
∠OFE = ∠OFK
∠OEF = ∠OKF
∠EOF = ∠KOF
Что и требовалось доказать.
б) ∠EFK - это вписанный угол, опирающийся на дугу FK. .
∠OFK - это центральный угол на той же дуге FK.
Центральный угол в 2 раза больше вписанного угла, опирающегося на ту же дугу.
Если ∠EFK = 80°, то ∠OFK = 2*80° = 160°