Задача 71994 ...

648551f2fb2b923089102132

11.06.2023 07:49:00

Через начало координат провести прямую, отстоящую от точки (2, −3) на расстоянии 9/√17,

5f3ea7e3faf909182968ddd9

11.06.2023 12:44:04

★

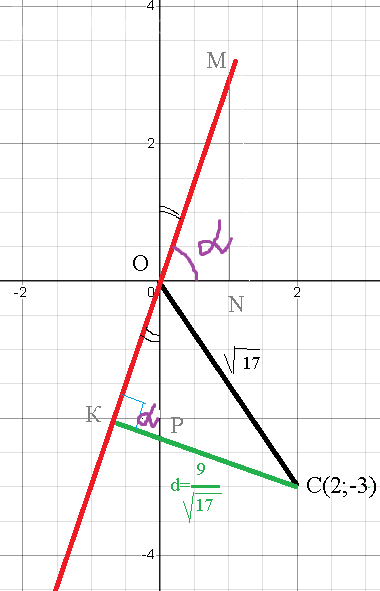
По условию, прямая проходит через начало координат (0;0)

Уравнение прямой с угловым коэффициентом k

y=kx+b

k=tg α

α - угол, который образует искомая прямая с осью Ох


Дано:
Расстояние от точки C(2;-3) до начала координат.
Оно равно

OC=sqrt((2-0)^2+(-3-0)^2)=sqrt(17)

cos ∠ OCK=KC/OC=9/17

OK^2=OC^2-CK^2=(sqrt(17))^2-(9/sqrt(17))^2=289-81/17=208/17

OK=2sqrt(52/17)


пусть K(x_(К);y_(К))

Тогда
x^2_(К)+y^2_(К)=208/17