Задача 71929 Дана функция z = f (x; y). Проверить,...
Условие
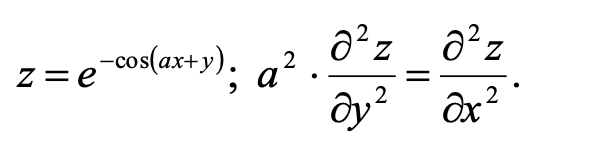
Решение
[m]\frac{ ∂z }{ ∂x }=(e^{-cos(ax+y)})`_{x}=e^{-cos(ax+y)}\cdot (cos(ax+y))`_{x}=-sin(ax+y)\cdot(ax+y)`_{x}\cdot e^{-cos(ax+y)}=-asin(ax+y)\cdot e^{-cos(ax+y)}[/m]
[m]\frac{ ∂z }{ ∂y }=(e^{-cos(ax+y)})`_{y}=e^{-cos(ax+y)}\cdot (cos(ax+y))`_{y}=(-sin(ax+y)\cdot(ax+y)`_{y}\cdot e^{-cos(ax+y)}=-sin(ax+y)\cdot e^{-cos(ax+y)}[/m]
[m]\frac{ ∂^2z }{ ∂x^2 }=(\frac{ ∂z }{ ∂x })`_{x}=(-asin(ax+y)\cdot e^{-cos(ax+y)})`_{x}=(-asin(ax+y))`_{x}\cdot e^{-cos(ax+y)}+(-asin(ax+y))\cdot (e^{-cos(ax+y)})`_{x}=[/m]
[m]=-acos(ax+y)\cdot (ax+y)`_{x}\cdot e^{-cos(ax+y)}+(-asin(ax+y))\cdot e^{-cos(ax+y)}\cdot (cos(ax+y))`_{x}=[/m]
[m]=-a^2cos(ax+y)\cdot e^{-cos(ax+y)}+(-asin(ax+y))\cdot(-asin(ax+y)\cdot e^{-cos(ax+y)})=a^2e^{-cos(ax+y)}\cdot (sin^2(ax+y)-cos(ax+y))[/m]
[m]\frac{ ∂^2z }{ ∂y^2 }=(\frac{ ∂z }{ ∂y })`_{y}=(-sin(ax+y)\cdot e^{-cos(ax+y)})`_{y}=(-sin(ax+y))`_{y}\cdot e^{-cos(ax+y)})+(-sin(ax+y)\cdot (e^{-cos(ax+y)})`_{y}=[/m]
[m]=-cos(ax+y)\cdot e^{-cos(ax+y)}+(-asin(ax+y))\cdot(-asin(ax+y)\cdot e^{-cos(ax+y)})= e^{-cos(ax+y)}\cdot (sin^2(ax+y)-cos(ax+y))[/m]
Подставляем в уравнение:
[m]a^2\cdot e^{-cos(ax+y)}\cdot (sin^2(ax+y)-cos(ax+y))=a^2e^{-cos(ax+y)}\cdot (sin^2(ax+y)-cos(ax+y))[/m]- верно