Задача 7175 Высота правильной четырёхугольной...

SvetaLyubimova

27.02.2016

Высота правильной четырёхугольной пирамиды равна 4, а сторона основания равна 6. Около основания пирамиды описана окружность.
а) Докажите, что отношение длины этой окружности к стороне основания равно Pisqrt(2)
б) Найдите площадь боковой поверхности конуса, основанием которого служит эта окружность, а вершина совпадает с вершиной пирамиды.

А)L=2piR
R=a/ sqrt(2)=6 sqrt(2)
L=(12pi)/ sqrt(2)
((12pi)/ sqrt(2))/6=pi sqrt(2)
Ч.т.д
Б) S бок=piRl
Образующая l=sqrt(34)
S=(pi6 sqrt(34))/ sqrt(2)=6pi sqrt(17)



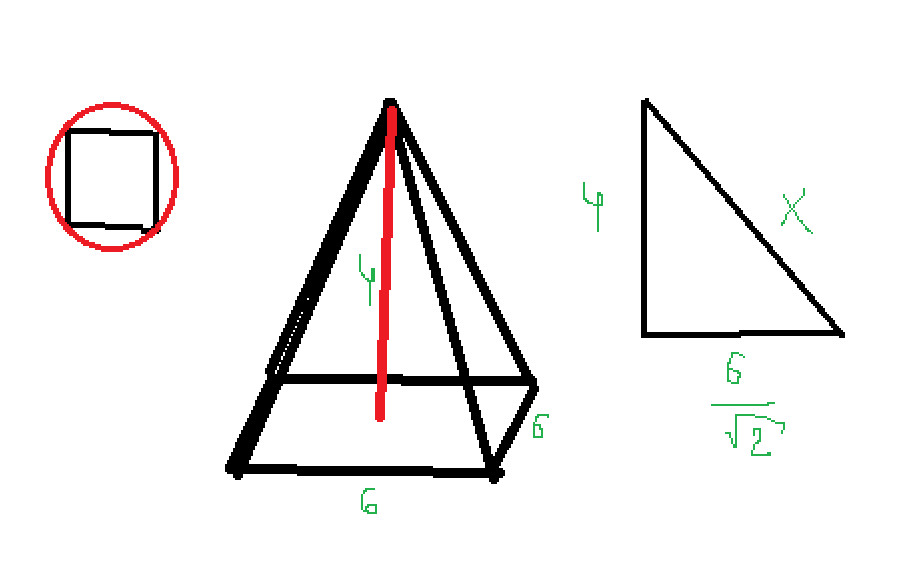
Ответ: а)pi sqrt(2) б)6pi sqrt(17