Задача 71681 дано:а(-4;2;5) б(8;-2;7) и с=а+б....
Условие
и с=а+б. Найдите угол между векторами a и c 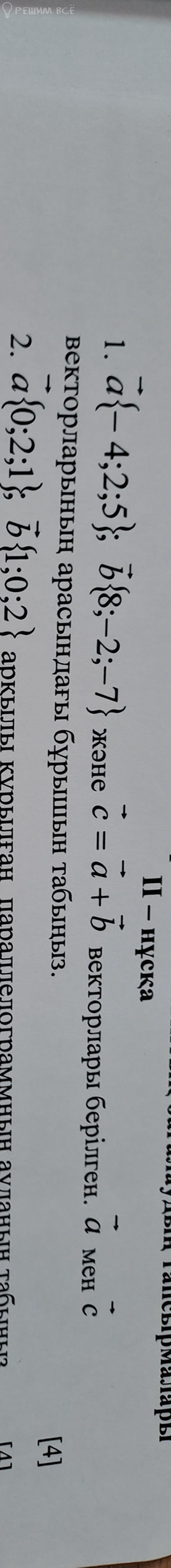
нет в списке 10-11 класс
222
Решение
★
с = a + b = (-4+8; 2-2; 5-7) = (4; 0; -2)
Нужно найти угол между векторами а и с.
[m]cos(φ) = \frac{x1x2+y1y2+z1z2}{\sqrt{x1^2+y1^2+z1^2} \cdot \sqrt{x2^2+y2^2+z2^2}} = \frac{(-4) \cdot 4+2 \cdot 0+5(-2)}{\sqrt{(-4)^2+2^2+5^2} \cdot \sqrt{4^2+0^2+(-2)^2}} = [/m]
[m]=\frac{-16+0-10}{\sqrt{16+4+25} \cdot \sqrt{16+0+4}} =\frac{-26}{\sqrt{45} \cdot \sqrt{20}}= -\frac{26}{3\sqrt{5} \cdot 2\sqrt{5}} = -\frac{26}{3 \cdot 2 \cdot 5} = -\frac{13}{15}[/m]
φ = π - arccos(13/15) ≈ π - π/6 = 5π/6 = 150°
Как ни удивительно, но 13/15 = 0,866666 ≈ sqrt(3)/2 = 0,866025
Ответ: ≈ 5π/6 = 150°