Задача 71640 Исследовать на условную сходимость и...
Условие
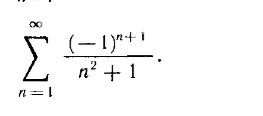
математика ВУЗ
168
Решение
★
∑ [m]\frac{1}{n^2+1}[/m] сходится, потому что эквивалентен ∑ [m]\frac{1}{n^2}[/m] - обобщенный гармонический ряд вида:
∑ [m]\frac{1}{n^{p}}[/m], который сходится при p>1 и расходится при p ≤ 1
Данный ряд сходится абсолютно