Задача 71224 x^(2) - |x + a + 3| = |x - a - 3| - (a +...

6416eb6b7a17db239744cebb

04.05.2023 19:39:12

x^(2) - |x + a + 3| = |x - a - 3| - (a + 3) ^2
Найти все значения а, при которых уравнение имеет единственный корень.

5f3ea7e3faf909182968ddd9

04.05.2023 21:56:17

★

О т в е т. При a=-5; a=-4;a=-3;a=-2 система имеет единственное решение

Решение:

x^2 – |x + a + 3| = |x – a – 3| – (a + 3)^ 2

Раскрываем модуль по определeнию


1)
x + a + 3 ≥ 0 ⇒ |x + a + 3| =x + a + 3
x – a – 3 ≥ 0 ⇒ |x - a - 3| =x - a - 3

Тогда уравнение принимает вид
x^2 – (x + a + 3) = (x – a – 3) – (a + 3)^ 2
Все условия должны выполняться одновременно, поэтому система:

[m]\left\{\begin {matrix}x + a + 3 ≥ 0\\
x – a – 3 ≥ 0\\x^2 –(x + a + 3) = x – a – 3 – (a + 3)^ 2\end {matrix}\right.[/m]

[m]\left\{\begin {matrix}x + 3 ≥ -a\\
x – 3 ≥a\\x^2 -2x + (a + 3)^ 2=0\end {matrix}\right.[/m]

Вводим в рассмотрение [i]координатно-параметрическую плоскость
[/i]
По оси Ох как обычно х
По оси Оу параметр а

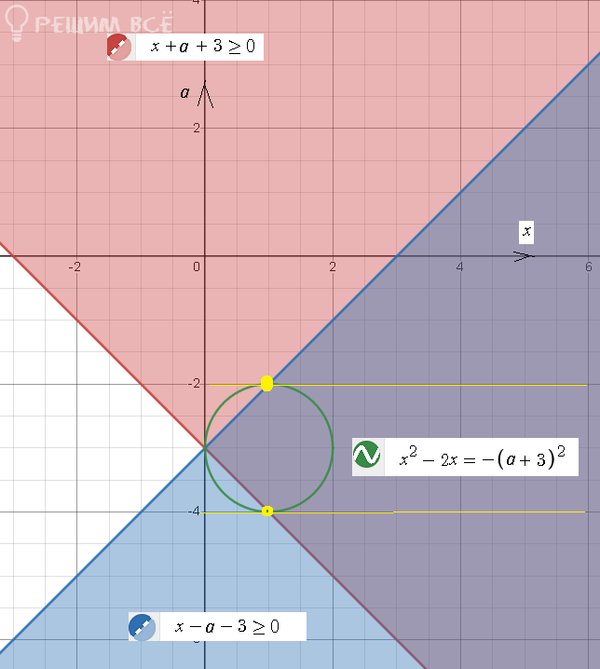
Cм геометрическую интерпретацию первого случая:
Это часть круга на сиреневой области


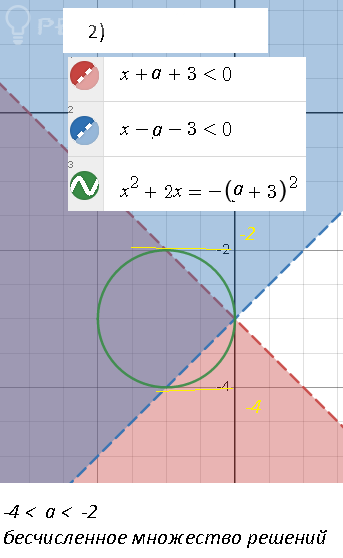
При -4 <a < -2
cистема имеет бесчисленное множество решений

При a=-4 и a=-2 система имеет единственное решение

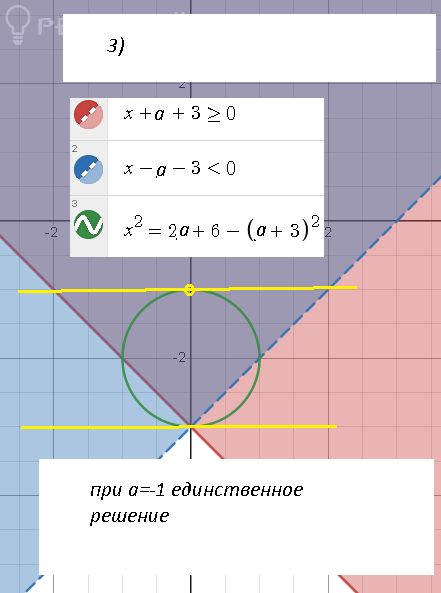
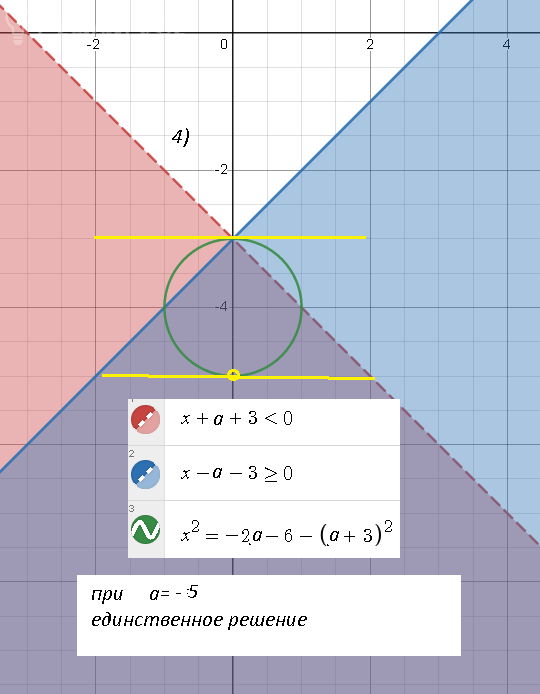
Аналогично рассматриваем три других случая