Задача 71124 неопределенный интеграл (4x-1) / (x^2...
Условие
неопределенный интеграл
(4x-1) / (x^2 +4x +3 ) dx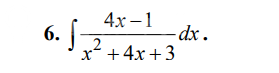
130
Решение
★
Выделяем полный квадрат в квадратном трехчлене
[m]x^2+4x+3=x^2+4x+4-1=(x+2)^2-1[/m]
Замена переменной
[m]x+2=t[/m] ⇒ [m]x=t-2[/m]
[m]dx=dt[/m]
[m] ∫ \frac{4x-1}{x^2+4x+3}dx= ∫\frac{4\cdot (t-2)-1}{t^2-1}dt =∫ \frac{4t-9}{t^2-1}dt= [/m]
[m]=∫ \frac{4t}{t^2-1}dt-∫ \frac{9}{t^2-1}dt =2ln|t^2-1|-9\cdot \frac{1}{2}ln|\frac{t-1}{t+1}|+C=[/m]
[m]=2ln|x^2+4x+3|- \frac{9}{2}ln|\frac{x+2-1}{x+2+1}|+C[/m]