Задача 71118 На рисунке прямая АС касается окружности...
Условие
20 баллов.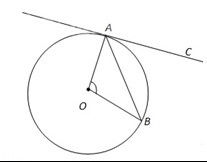
693
Решение
★
∠ОАВ= ∠ОВА=(180^(o)- ∠АОВ):2=(180^(o)-96^(o)):2=42^(o).
Радиус, проведенный в точку касания, перпендикуляре касательной: ОА ⊥ АС.
Тогда ∠САВ=90^(o)- ∠ОАВ=90^(o)-42^(o)=48^(o).
Ответ: 48^(o).