Задача 71097 При каких значениях параметра а...

6209ed38eb82603b2a8ab478

28.04.2023 10:44:00

При каких значениях параметра а уравнение
x
3
+
a
x
2
+
13
x
−
6
=
0
имеет единственное решение?

5f3ea7e3faf909182968ddd9

28.04.2023 10:50:43

★

x^3+ax^2+13x-6=0

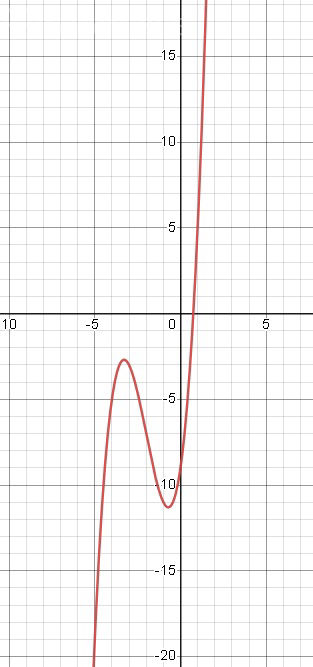
Уравнение имеет единственное решение, если кривая y=x^3+ax^2+13x-6 пересекает ось Ох в одной точке

Значит функция y=x^3+ax^2+13x-6 монотонно возрастает

y`=3x^2+2ax+13

y`>0

D <0

D=(2a)^2-4*3*13

⇒

a^2-52 <0

[b]-2sqrt(13) < a < 2sqrt(13)[/b]


или

точки максимума и минимума расположены ниже оси Ох ( см. рис.)

D=(2a)^2-4*3*13=4*(a^2-52)

⇒

x_(1)=(-2a-2sqrt(a:2-52))/2 ; x_(2)=(-2a+2sqrt(a:2-52))/2

x_(1)=-a-sqrt(a^2-52) ; x_(2)=-a+sqrt(a^2-52)

Значения а находим из системы:

{y(x_(1)) <0
{y(x_(2)) <0

получим второй ответ

О т в е т. Объединяем оба ответа