Задача 71090 integrate (3x + 5) * ln(3x + 5) dx...
Условие
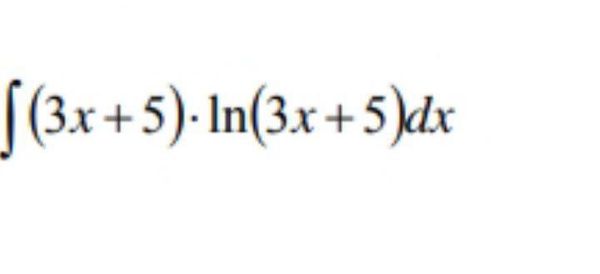
120
Решение
★
u=ln(3x+5)
du=3dx/(3x+5)
dv=(3x+5)dx
v=(3x^2/2)+5x
∫ (3x+5)ln(3x+5)dx=(ln(3x+5))*((3x^2/2)+5x)- ∫((3x^2/2)+5x)*(3dx/(3x+5)=
=((3x^2/2)+5x)*ln(3x+5)-(3/2) ∫ (3x^2+10x)dx/(3x+5)=
под интегралом неправильная дробь, выделяем целую часть:
=((3x^2/2)+5x)*ln(3x+5)-(3/2) ∫[b] ([/b](x+(5/3)- (25/3)*(1/(3x+5))[b])[/b]dx=
=((3x^2/2)+5x)*ln(3x+5)-(3/2)*[b]([/b](x^2/2)+(5/3)*x-(25/3)*(1/3)*ln|5x+3|[b])[/b]+C