Задача 71088 integrate (10x - 9)/(2x ^ 2 - 6x + 30)...
Условие
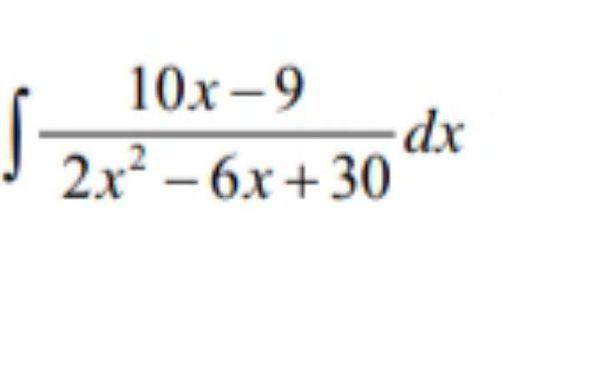
94
Решение
★
2x^2-6x+30=2*(x^2-3x+15)=2*((x-1,5)^2+12,75)
замена переменной
x-1,5=t
x=t+1,5
dx=dt
∫ (10x-9)dx/2*((x-1,5)^2+12,75)=(1/2) ∫ (10t+6)dt/(t^2+12,75)=(5/2) ∫2tdt/(t^2+12,75) +3 ∫ dt/((t^2+12,75)
Первый интеграл табличный
∫ du/u=ln|u|
u=t^2+12,75
du=2tdt
Второй интеграл табличный
∫ dt/(t^2+a^2)=(1/a)arctg (t/a)
=(5/2)ln|t^2+12,75)|+3*(1/sqrt(12,75))arctg (t/sqrt(12,75) + C
12,75=12(3/4)=51/4
sqrt(12,75)=sqrt(51/4)=sqrt(51)/2
Обратная замена
=2,5 ln|x^2-3x+15|+6/sqrt(51)arctg(2x+3)/sqrt(51) + C