Задача 70693 ...

64301c835de158378856eb83

08.04.2023 22:29:17

Основание пирамиды SABCD с вершиной S является прямоугольник ABCD, причем SB=BC=√2·AB. Диагонали прямоугольника ABCD пересекаются в точке O. Отрезок SO является высотой пирамиды SABCD. Из вершины A опущены перпендикуляры AP и AQ на ребра SB и SD соответственно.
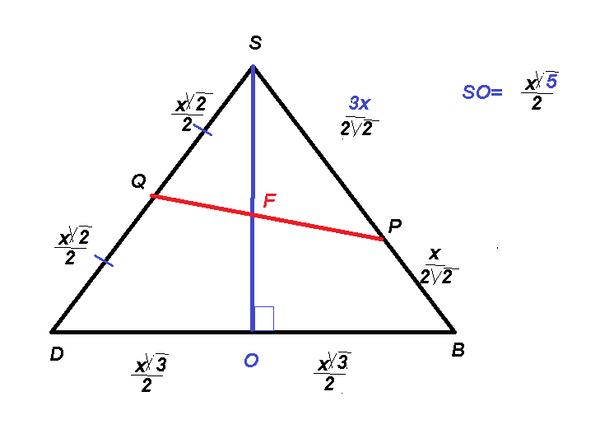
а) Докажите, что прямая PQ делит высоту пирамиды в отношении 3/2, считая от точки S.
б) Найдите двугранный угол пирамиды при ребре SB

5f3ea7e3faf909182968ddd9

09.04.2023 20:20:17

★

В основании пирамиды прямоугольник.
причем
BC=√2·AB.

Пусть FD=CD=x
BC=AD=x*sqrt(2)

Диагонали прямоугольника [i]равны[/i] и в точке пересечения делятся [i]пополам[/i]
AC=BD=x*sqrt(3)

АО=ВО=СО=DO=x*sqrt(3)/2


SO ⊥ пл. АВСD

АО - проекция SA.

Значит SA=SB=SC=SD=x*sqrt(2) ( равные проекции имеют равные наклонные)

[b]a) [/b]Δ SAB - равнобедренный (SA=SB)

По условию AP ⊥ SB

Пусть BP=t
тогда РС=х*sqrt(2)-t

Из Δ АВР

АР^2=x^2-t^2

Из Δ АРC

AP^2=(x*sqrt(2))^2-(x*sqrt(2)-t)^2

Приравниваем правые части

x^2-t^2=(x*sqrt(2))^2-(x*sqrt(2)-t)^2

x^2-t^2=2*x^2-(2*x^2-2*x*sqrt(2)*t+t^2)

t=x/2sqrt(2)

АР^2=x^2-t^2=x^2-(x/2sqr(2))^2=7x^2/8

[b]AP=x*sqrt(7)/(2sqrt(2))[/b]


Δ SAD - равносторонний (SA=SD=AD=x*sqrt(2))

По условию AQ ⊥ SD

AQ=x*sqrt(2)*sqrt(3)/2=x*sqrt(6)/2

SQ=QD=x*sqrt(2)/2

Δ SBС - равнобедренный (SВ=SС=x*sqrt(2))

CK ⊥ SB

CK=AQ=x*sqrt(2)*sqrt(3)/2=x*sqrt(6)/2

PM || СK

Δ BPM ∼ Δ ВСК

ВР : KB=PM : CK

t : x*sqrt(2)/2=PM: x*sqrt(6)/2

t=x/(2sqrt(2))


PM=x*sqrt(6)/4

ВМ^2=BP^2+PM^2
BM=(x/(2sqrt(2))^2+(x*sqrt(6)/4)^2
BM^2=x^2/8
BM=x/(2sqrt(2))


б)

∠ APM -[i] линейный угол [/i]двугранного угла при ребре SB

Стороны треугольника АРM.

BM=x/(2sqrt(2))

АМ^2=MB^2+AB^2
АМ^2=(x/(2sqrt(2)))^2+x^2=9x^2/8

АМ=3x/(2sqrt(2))

[b]AP=x*sqrt(7)/(2sqrt(2))[/b]

По теореме косинусов

AM^2=AP^2+PM^2-2*AP*PM*cos∠ APM

cos∠ APM =