Задача 70681 Гипотенуза прямоугольного треугольника...

6397808b1f425c75901ed259

07.04.2023 21:39:34

Гипотенуза прямоугольного треугольника равна 5, а высота проведенная к ней равна 2. Найдите радиусы вписанной и описанной окружностей.

5f3ea7e3faf909182968ddd9

07.04.2023 23:34:36

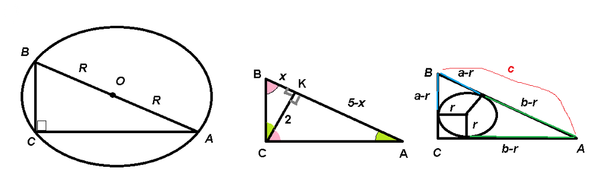
Прямой угол С опирается на диаметр ( cм. рис. 1)
Гипотенуза прямоугольного треугольника - диаметр описанной окружности
R=(1/2)c=(1/2)*5=2,5

Рис. 2
Высота проведенная к гипотенузе равна 2.

Δ АСК ∼ Δ BCK
по двум углам

ВК:СК=СК:КА
ВК=х;
КА=5-х
х:2=2:(5-х)
х*(5-х)=2*2
х^2-5x+4=0
D=25-16=9
x=1 или x=4
5-x=4 или 5-x=1
высота делит гипотенузу на отрезки 1 и 4
или 4 и 1

Выбираем соответственно рисунка
ВK=1
AK=4

АС^2=CK^2+KA^2
AC^2=2^2+4^2=20
AC=sqrt(20)=2sqrt(5)
BC^2=AB^2-AC^2=25-20=5
BC=sqrt(5)


По свойству касательных к окружности, проведенных из одной точки, отрезки касательных равны ( см. рис.3)

⇒

[m]с=a-r+b-r[/m]

[m]c=a+b-2r[/m]

[m]r=\frac{a+b-c}{2}=\frac{2\sqrt{5}+\sqrt{5}-5}{2}=\frac{3\sqrt{5}-5}{2}[/m]

О т в е т. R=2,5; r=[m]\frac{3\sqrt{5}-5}{2}[/m]