Задача 70546 Исследовать методами дифференциального...
Условие
y = f(x)
и, используя результаты исследования, построить ее график.
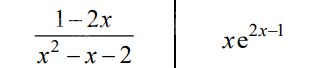
Решение
[m]y = f(x) = \frac{1 - 2x}{x^2 - x - 2}[/m]
1) Область определения:
x^2 - x - 2 ≠ 0
(x + 1)(x - 2) ≠ 0
x ≠ -1; x ≠ 2
[b]D(X) = (-oo; -1) U (-1; 2) U (2; +oo)[/b]
Оба разрыва - неустранимые 2 рода.
2) Вертикальные асимптоты:
[b]x = -1; x = 2[/b]
3) Пересечение с осями координат.
С осью Oy: x = 0.
[m]y = f(0) = \frac{1 - 0}{0 - 0 - 2} = \frac{1}{-2} = -0,5[/m]
[b]M1(0; -0,5)[/b]
С осью Ox: y = 0
1 - 2x = 0
2x = 1
x = 1/2 = 0,5
[b]M2(0,5; 0)[/b]
4) Четность функции:
[m]f(-x) = \frac{1 + 2x}{x^2 + x - 2}[/m]
f(-x) ≠ -f(x); f(-x) ≠ f(x)
[b]Функция не чётная и не нечётная.[/b]
5) Периодичность функции:
[b]Функция не периодическая.[/b]
6) Критические точки. Точки, в которых y' = 0 или не существует.
[m]y' = \frac{-2(x^2-x-2) - (1 - 2x)(2x - 1)}{(x^2-x-2)^2} = \frac{-2x^2+2x+4+4x^2-4x+1}{(x^2-x-2)^2} =[/m]
[m] = \frac{2x^2-2x+5}{(x^2-x-2)^2}=0[/m]
2x^2 - 2x + 5 = 0
D = (-2)^2 - 4*2*5 = 4 - 40 = -36 < 0
[b]Точек экстремума нет. [/b]
Точки, в которых y' не существует: x1 = -1; x2 = 2
Промежутки возрастания и убывания функции:
[m] y' = \frac{2x^2-2x+5}{(x^2-x-2)^2}[/m]
Числитель 2x^2 - 2x + 5 > 0 при любом x.
Знаменатель (x^2 - x - 2)^2 > 0 при любом x ∈ Области определения.
[b]Функция возрастает на всей области определения.[/b]
7) Точки перегиба. Это точки, в которых y'' = 0 или не существует.
[m]y'' = \frac{(4x - 2)(x^2-x-2)^2 - 2(2x^2-2x+5)(x^2-x-2)(2x-1)}{(x^2-x-2)^4} = \frac{(4x - 2)(x^2-x-2) - 2(2x^2-2x+5)(2x-1)}{(x^2-x-2)^3} = [/m]
[m]= \frac{2(2x - 1)(x^2-x-2) - 2(2x-1)(2x^2-2x+5)}{(x^2-x-2)^3} = \frac{2(2x - 1)(x^2-x-2-2x^2+2x-5)}{(x^2-x-2)^3} = \frac{2(2x - 1)(-x^2+x-7)}{(x^2-x-2)^3} = 0[/m]
2(2x - 1)(-x^2 + x - 7) = 0
2x - 1 = 0
x1 = 1/2 = 0,5; y(0,5) = 0 (см. п. 3)
[b]M2(0,5; 0)[/b] - точка перегиба.
-x^2 + x - 7 = 0 - это уравнение корней не имеет.
Точки, в которых y'' не существует: x1 = -1; x2 = 2
Промежутки выпуклости и вогнутости функции:
При x < -1 будет y'' > 0 - функция вогнутая
При x ∈ (-1; 0,5) будет y'' < 0 - функция выпуклая
При x ∈ (0,5; 2) будет y'' > 0 - функция вогнутая
При x > 2 будет y'' < 0 - функция выпуклая
8) Наклонные асимптоты.
g(x) = kx + b
[m]k = \lim \limits_{x \to \infty} \frac{f(x)}{x} = \lim \limits_{x \to \infty} \frac{1 - 2x}{x^3 - x^2 - 2x} = 0[/m]
[m]b = \lim \limits_{x \to \infty} (f(x - k \cdot x)) = \lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} \frac{1 - 2x}{x^2 - x - 2} = 0[/m]
Горизонтальная асимптота: [b]g(x) = 0[/b], то есть ось Ox.
9) Область значений функции
[b]E(Y) = (-oo; +oo)[/b]
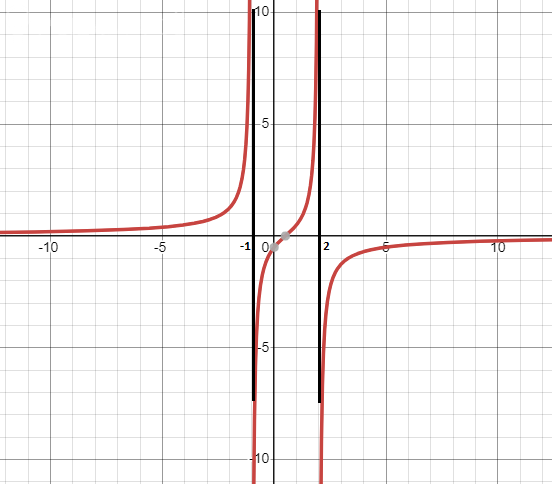
10) График прилагается. Вертикальные асимптоты показаны черным.