Задача 70534 Треугольник со сторонами 5 см, 29 см и...

63d026bcf0b2d702a30855bc

02.04.2023 13:14:20

Треугольник со сторонами 5 см, 29 см и 30 см вращается вокруг большей стороны. Найдите объем и площадь поверхности тела вращения,
что при этом образовалось.

5f3ea7e3faf909182968ddd9

02.04.2023 13:58:10

★

Получилось два конуса одинакового радиуса ОС
Конус 1:
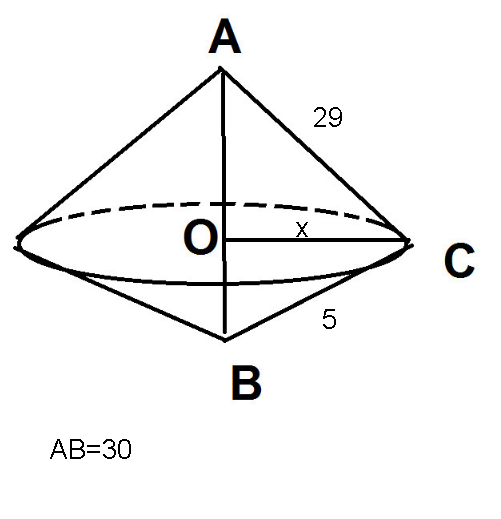
L=AC=29
R=ОС
Конус 2:
L=BC=5
R=ОС
S_(тела вращения)=S_( конуса _(1))+S_( конуса _(2))=π*R*L_(1)+π*R*L_(2)


1 способ

Пусть ОС=х

AO^2=AC^2-OC^2=29^2-x^2 ⇒ AO=sqrt(29^2-x^2)

BO^2=BC^2-)C^2=5^2-x^2 ⇒ BO=sqrt(5^2-x^2)

AO+OB=30

Уравнение:

sqrt(29^2-x^2)+sqrt(5^2-x^2)=30
Иррациональное уравнение .

Перепишем в виде:

sqrt(29^2-x^2)=30-sqrt(5^2-x^2)

возводим в квадрат:

29^2-x^2=30^2-2*30*sqrt(25-x^2)+25-x^2
29^2=30^2-2*30*sqrt(25-x^2)+25
60*sqrt(25-x^2)=30^2-29^2+25
60*sqrt(25-x^2)=(30-29)(30+29)+25
60*sqrt(25-x^2)=59+25
60*sqrt(25-x^2)=84
sqrt(25-x^2)=7/5

25-x^2=(7/5)^2
x^2=25-(7/5)^2
x^2=(625-49)/5^2
[red][b]x=24/5[/b][/red]


2 способ

Пусть ОВ=y
тогда
АО=30-y

OC^2=AC^2-AO^2=29^2-(30-y)^2

OC^2=BC^2-OB^2=5^2-y^2

OC^2=OC^2

Уравнение
29^2-(30-y)^2 =5^2-y^2

29^2-5^2=(30-y)^2-y

(29-5)*(29+5)=(30-y-y)*(30-y+y)

24*34=30*(30-2y)

24*34=60*(15-y)


15-y=204/15

y=(225-204)/15


y=21/15

y=7/5


R^2=5^2-(7/5)^2=(625-49)/25

[red][b]R=24/5[/b][/red]


S_(тела вращения)=S_( конуса _(1))+S_( конуса _(2))=π*R*L_(1)+π*R*L_(2)


S_(тела вращения)==π*R*(L_(1)+L_(2))=π*[red][b]24/5[/b][/red]*(29+5)= кв см