Задача 70531 Функция u = f(x;y) задана неявно...
Условие
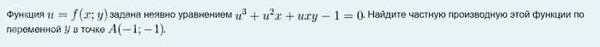
ВУЗ
132
Решение
★
Заметим, что u'_(y) = u'_(y); y'_(y) = 1; x'_(y) = 0
Производная от неявной функции:
3u^2*u'_(y) + 2u*x*u'_(y) + u'_(y)*x*y + u*x*y'_(y) - 0 = 0
u'_(y)*(3u^2 + 2u*x + x*y) + u*x = 0
u'_(y) = -u*x/(3u^2 + 2u*x + x*y)