Задача 70446 Дана трапеция KLMN с основаниями КN и...

63fbb8ff4e2b240cfe0d528e

28.03.2023 19:39:13

Дана трапеция KLMN с основаниями КN и LМ. Диагональ LN разбивает её на два равнобедренных треугольника с основаниями КN и МN.

а) Докажите, что луч КМ — биссектриса угла LКN.
б) Найдите МN, если известны диагонали трапеции: KM = 20, LN =10,5.

5f3ea7e3faf909182968ddd9

28.03.2023 22:05:52

★

a)
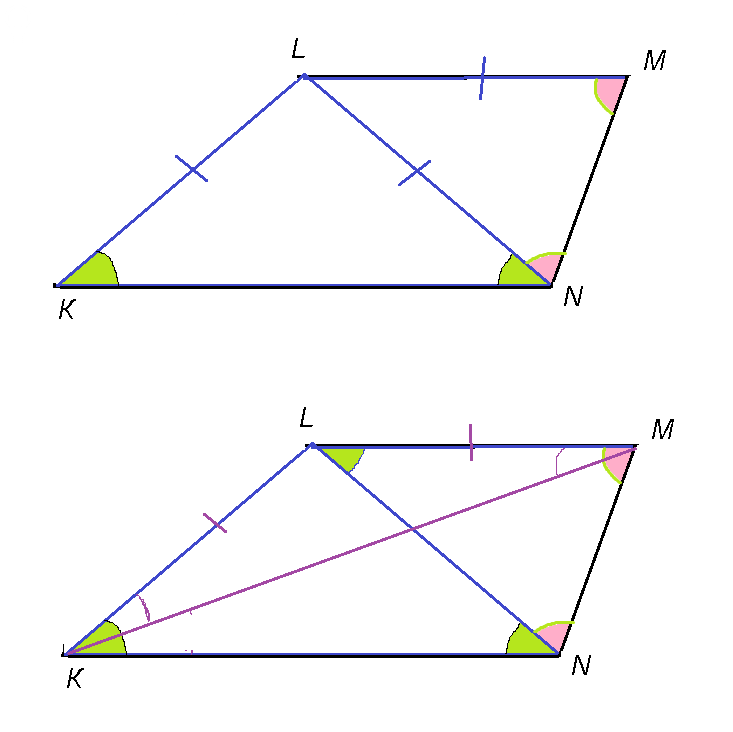
рис. 1
Δ KLN - равнобедренный с основанием KN
KL=LN ⇒ ∠ LKN= ∠ LNK

Δ LMN - равнобедренный с основанием MN
LN=LM ⇒ ∠ LMN= ∠ LNM

рис. 2
Δ KLM - равнобедренный с основанием KM
LK=LM ⇒ ∠ LKM= ∠ LMK

∠ MKN= ∠LMK - внутренние накрест лежащие

∠ LKM=∠ MKN

⇒ KM -[i] биссектриса[/i] ∠ LKN

б)
Δ KLM - равнобедренный
KL=LM=10,5
KL=20

По теореме косинусов:
LM^2=KL^2+KM^2-2*KL*KM*cos ∠ KML

cos ∠ KML=20/21

⇒ ∠ NLM=2∠ KML

cos∠ NLM=2cos^2∠ KML-1=2*(20/21)^2-1=359/441

(cos2 α =2cos^2 α -1)

⇒

по теореме косинусов

MN^2=10,5^2+10,5^2-2*10,5*10,5*(359/441)=...