Задача 70361 найти сумму числового ряда (с...
Условие
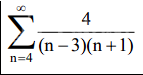
Решение


Все решения
[m]\frac{4}{(n-3)(n+1)}=\frac{A}{n-3}+\frac{B}{n+1}[/m]
[m]\frac{4}{(n-3)(n+1)}=\frac{A(n+1)}{(n-3)(n+1)}+\frac{B(n-3)}{(n-3)(n+1)}[/m]
[m]\frac{4}{(n-3)(n+1)}=\frac{A(n+1)+B(n-3)}{(n-3)(n+1)}[/m]
Приравниваем числители:
[m]4=A(n+1)+B*(n-3)[/m]
При n=3
[m]4=A*4+B*0[/m] ⇒[m]A=1[/m]
При n=4
[m]4=1*5+B*1[/m] ⇒ [m]B=-1[/m]
[m]\frac{4}{(n-3)(n+1)}=\frac{1}{n-3}-\frac{1}{n+1}[/m]
Тогда ряд можно записать в виде
[m] ∑^{ ∞}_{n=4} (\frac{1}{n-3}-\frac{1}{n+1})[/m]
Найдем n-ую частичную сумму
[m]S_{n}=\underbrace{(\frac{1}{4-3}-\frac{1}{4+1})}_{a_{4}}+\underbrace{(\frac{1}{5-3}-\frac{1}{5+1})}_{a_{5}}+\underbrace{(\frac{1}{6-3}-\frac{1}{6+1})}_{a_{6}}+... +\underbrace{(\frac{1}{n-1-3}-\frac{1}{n-1+1})}_{a_{n-1}}+\underbrace{(\frac{1}{n-3}-\frac{1}{n+1})}_{a_{n}} [/m]
[m]S_{n}=1+\frac{1}{2}+\frac{1}{3}-\frac{1}{n}-\frac{1}{n+1}[/m]
[m]S=lim_{n → ∞ }S_{n}=lim_{n → ∞ }(1+\frac{1}{2}+\frac{1}{3}-\frac{1}{n}-\frac{1}{n+1})=\frac{11}{6}-0-0=\frac{11}{6}[/m]