Задача 70359 3. На кривой — у=3^(x)+3х? +4х найти...

637cdb0504ff381bf0bedd34

24.03.2023 13:41:41

3. На кривой — у=3^(x)+3х? +4х найти точку, в которой касательная- параллельна биссектрисе первого координатного угла. записать уравнение этой касательной

626fab9a354ab65fb2f43abb

24.03.2023 17:31:20

★

y = x^3 + 3x^2 + 4x
Биссектриса первого координатного угла - это прямая y = x.
Надо найти касательную, параллельную этой прямой.
Значит. уравнение касательной: f(x) = x + b
Остается найти свободный член b.
Уравнение касательной в точке x0:
f(x) = y(x0) + y'(x0)*(x - x0)
y'(x) = 3x^2 + 6x + 4
y'(x0) = 3x0^2 + 6x0 + 4 = 1
3x0^2 + 6x0 + 3 = 0
3(x0^2 + 2x0 + 1) = 0
3(x0 + 1)^2 = 0
x0 = -1
y(-1) = (-1)^3 + 3(-1)^2 + 4(-1) = -1 + 3 - 4 = -2
Уравнение касательной:
f(x) = -2 + 1(x + 1)
f(x) = -2 + x + 1
f(x) = x - 1
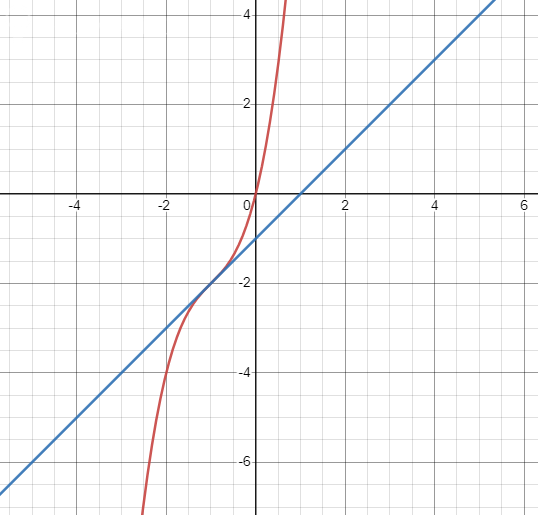
График прилагается.