Задача 70288 Нужна помощь, не понимаю вообще эту...
Условие

Решение
S(тр) = 1/2*AB*BC*sin ABC = 1/2*4*5*sin 60° = 10*sqrt(3)/2 = 5sqrt(3) см^2
2) Половина ромба - это равнобедренный треугольник.
S(рб) = 2*S(тр) = 2*1/2*8*8*sin 135° = 64*sqrt(2)/2 = 32sqrt(2) см^2
3) AB = 6 см, ∠A = 30°; ∠B = 45°
∠С = 180° - 30° - 45° = 105°
По теореме синусов:
BC/sin A = AC/sin B = AB/sin С
AB/sin С = 6/sin 105° ≈ 6/0,966 ≈ 6,2117
BC/sin A = 6,2117
BC = 6,2117*sin A = 6,2117*sqrt(3)/2 ≈ 5,38 см
AC/sin B = 6,2117
AC = 6,2117*sin B = 6,2117*sqrt(2)/2 ≈ 4,39 см
4) Один угол пар-грамма равен 60°, значит, второй угол 120°.
Диагонали можно найти по теореме косинусов:
d1^2 = a^2 + b^2 - 2*a*b*cos 60° = 3^2 + 8^2 - 2*3*8*1/2 =
= 9 + 64 - 24 = 49 = 7^2
d1 = 7 см
d2^2 = a^2 + b^2 - 2*a*b*cos 120° = 3^2 + 8^2 - 2*3*8*(-1/2) =
= 9 + 64 + 24 = 97
d2 = sqrt(97) см
5) AB = 6 см, ∠A = 89°; ∠B = 31°
Найти радиус окружности, описанной вокруг треугольника.
∠C = 180° - 89° - 31° = 60°
По теореме синусов:
BC/sin A = AC/sin B = AB/sin С = 2R
R = AB/(2sin С) = 6 / (2*sqrt(3)/2) = 6/sqrt(3) = 6sqrt(3)/3 = 2sqrt(3) ≈ 3,464 см
6) AB = 10 см, BC = 17 см, AC = 21 см
Найти радиус окружности, вписанной в треугольник.
p = (AB + BC + AC)/2 = (10 + 17 + 21)/2 = 24 см
Площадь треугольника по формул Герона:
S = sqrt(p(p - AB)(p - BC)(p - AC)) = sqrt(24*14*7*3) = sqrt(8*3*2*7*7*3) =
= 4*3*7 = 84 см^2
С другой стороны, площадь можно найти так:
S = p*r
Отсюда радиус вписанной окружности:
r = S/p = 84/24 = 7/2 = 3,5 см
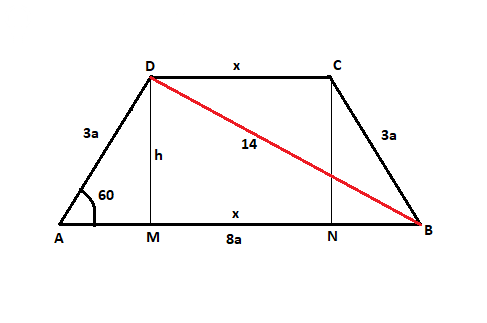
7) У равносторонней трапеции две боковых стороны равны.
Большое основание относится к длине боковой стороны как 8 : 3.
Обозначим большое основание 8a см, а боковые стороны 3a см.
Угол между большим основанием и боковой стороной равен 60°.
Диагональ трапеции равна 14 см.
Найти периметр трапеции.
Смотрите рисунок.
Малое основание обозначим x см.
AM = AD*cos 60° = 3a*1/2 = 1,5a
MN = CD = x = 8a - 2*1,5a = 5a
По теореме косинусов для треугольника ABD:
BD^2 = AB^2 + AD^2 - 2*AB*AD*cos 60° = 9a^2 + 64a^2 - 2*3a*8a*1/2 =
= 9a^2 + 64a^2 - 24a^2 = 49a^2
BD = 7a = 14 см
a = 2 см, BC = AD = 3a = 6 см, CD = 5a = 10 см, AB = 8a = 16 см.
Периметр трапеции:
P = 2*3a + 8a + 5a = 2*6 + 16 + 10 = 38 см