Задача 70215 Прямоугольный треугольник, катет...

63d026bcf0b2d702a30855bc

19.03.2023 22:12:52

Прямоугольный треугольник, катет которого равен 8 см, а гипотенуза – 10 см, вращается вокруг гипотенузы. Найдите объем тела, которое при этому образовалось.

5f3ea7e3faf909182968ddd9

20.03.2023 12:16:17

★

При вращении прямоугольного треугольника АВС вокруг гипотенузы АВ получим два конуса с радиусом основания
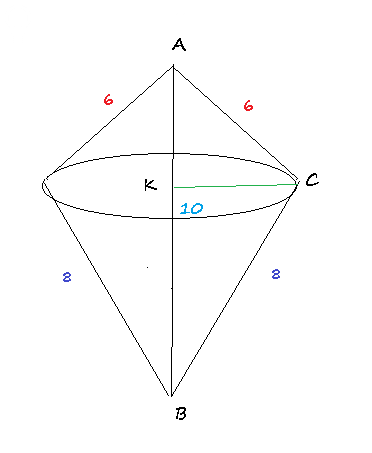
KC и высотами
H_(1)=АК
и
H_(2)=КB

В прямоугольном треугольнике АВС
АВ=10
ВС=8
По теореме Пифагора
AC^2=AB^2-BC^2=10^2-8^2=100-64=36
AC=6

KC ⊥ AB
KC- высота прямоугольного треугольника
S_( Δ ABC)=(1/2)*AC*BC
S_( Δ ABC)=(1/2)*AB*CK

⇒ =(1/2)*AB*CK=(1/2)*AC*BC

CK=AC*BC/AB=6*8/10=4,8

R=[b]4,8[/b]

V=V_(1)+V_(2)=(1/3)*π*R^2*H_(1)+(1/3)*π*R^2*H_(2)=(1/3)*π*R^2*(H_(1)+H_(2))=(1/3)*π*4,8^2*(AK+KB)=(1/3)*π*4,8^2*(AB)=(1/3)*π*4,8^2*10=