Задача 700 На рисунке представлен график...
Условие
1) 50 м 2) 100 м 3) 200 м 4) 250 м 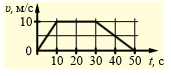
физика 10-11 класс
14198
Решение
Ответ: 4
Все решения
1) 50 м 2) 100 м 3) 200 м 4) 250 м 
Ответ: 4