Задача 69990 Найти неопределенные интегралы...
Условие
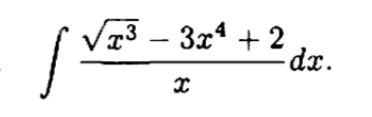

Решение
[m]\int \frac{\sqrt{x^3} - 3x^4 + 2}{x} dx = \int (\frac{x\sqrt{x}}{x} -3x^3 + \frac{2}{x}) dx = \int (\sqrt{x} -3x^3 + \frac{2}{x}) dx[/m]
Дальше берем интегралы от каждого слагаемого отдельно:
[m]\int x^{1/2} dx - 3\int x^3 dx + 2\int \frac{1}{x} dx = \frac{x^{3/2}}{3/2} - 3\frac{x^4}{4} + 2ln|x| + C= [/m]
[m] = \frac{2}{3} \sqrt{x^3} - 3\frac{x^4}{4} + 2ln|x| + C[/m]
Проверка:
[m](\frac{2}{3}\sqrt{x^3} - 3\frac{x^4}{4} + 2ln|x| + C)' = \frac{2}{3} \cdot \frac{3}{2} \cdot x^{1/2} - \frac{3}{4} \cdot 4x^3 + \frac{2}{x} = [/m]
[m] = \sqrt{x} - 3x^3 + \frac{2}{x} = \frac{x \sqrt{x}}{x} -3x^3 + \frac{2}{x} = \frac{\sqrt{x^3} -3x^4 + 2}{x}[/m]
2) Есть правило: [m]\int f(ax + b) dx = \frac{1}{a} \cdot F(ax+b) + C[/m]
[m]\int \sqrt[5]{3 - 2x}dx = \int (3-2x)^{1/5} dx = -\frac{1}{2} \cdot \frac{(3-2x)^{6/5}}{6/5} + C = -\frac{5}{12} \cdot (3-2x)^{6/5} + C [/m]
Проверка:
[m](-\frac{5}{12} \cdot (3-2x)^{6/5} + C)' = -\frac{5}{12} \cdot \frac{6}{5} \cdot (3-2x)^{1/5} \cdot (-2) =[/m]
[m]= -\frac{6}{12} \cdot (-2)\cdot \sqrt[5]{3 - 2x} = \sqrt[5]{3 - 2x}[/m]