Задача 69943 ...

6397808b1f425c75901ed259

09.03.2023 23:09:10

В треугольнике ABC: ∡C=10°,∡B=20°. Вне треугольника выбрана точка M так, что треугольник CMB – правильный (точки М и А лежат в разных полуплоскостях относительно ВС). Найдите ∠МАВ и МАС.

5f3ea7e3faf909182968ddd9

10.03.2023 00:26:35

★

ВС=ВМ=СМ=a

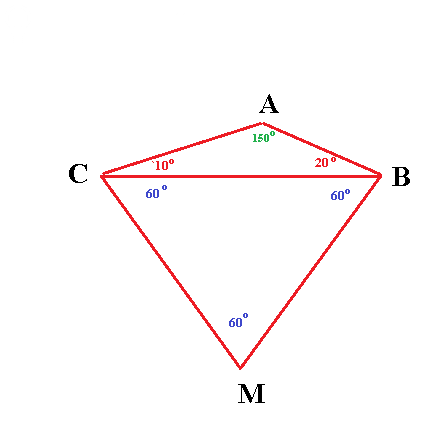
Пусть
АВ=x
АС=у

По теореме синусов из Δ АВС

a/sin150 ° =x/sin10 ° =y/sin20 °
sin150 ° =sin30=1/2
⇒
x=2a*sin10 °

y=2a*sin20 °


Из Δ АМВ по теореме косинусов:

АМ^2=(2a*sin10 ° )^2+a^2-2*(2a*sin10 ° )*a*cos80 °

cos80 ° =sin10 °


АМ^2=(2a*sin10 ° )^2+a^2-(2a*sin10 ° )^2=a^2

АМ=а

Δ АМВ - [i]равнобедренный[/i] ( АМ=BM) ⇒
∠ МАВ=80 °

Тогда
∠ МАС=150 ° -80 ° =70 °