Задача 69839 Продифференцировать данные функции ...
Условие
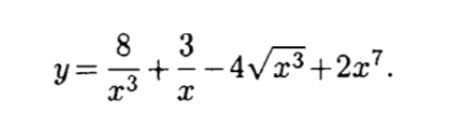
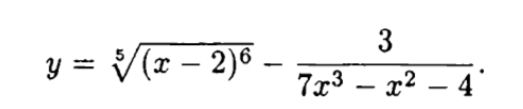
Решение
[m]y`=(\frac{8}{x^3}+\frac{3}{x}-4\sqrt[]{x^3}+2x^7)`=[/m]
производная суммы ( разности) равна сумме (разности) производных
[m]=(\frac{8}{x^3})`+(\frac{3}{x})`-(4\sqrt[]{x^3})`+(2x^7)`=[/m]
постоянный множитель можно выносить за знак производной:
[m]=8(\frac{1}{x^3})`+3(\frac{1}{x})`-4(\sqrt[]{x^3})`+2(x^7)`=[/m]
применяем свойства степени:
[m]=8(x^{-3})`+3(x^{-1})`-4(x^{\frac{3}{2}})`+2(x^7)`=[/m]
применяем формулы ( см таблицу производных):
[r][m] C`=0[/m];[/r]
[r][m](x^{ α })`= α \cdot x^{ α -1}[/m][/r]
[m]=8\cdot (-3)x^{-4}+3\cdot (-1)\cdot x^{-2} -4\cdot \frac{3}{2}\cdot x^{\frac{3}{2}-1}+2\cdot 7x^{6}[/m]
[m]=-\frac{24}{x^4}-\frac{3}{x^2}-6x^{\frac{1}{2}}+14x^6=-\frac{24}{x^4}-\frac{3}{x^2}-6\cdot \sqrt{x}+14x^6[/m]
2)
[m]y= ((x-2)^{\frac{6}{5}})`-3\cdot ((7x^3-x^2-4)^{-1})`[/m]
[m]y`=\frac{6}{5}\cdot (x-2)^{\frac{6}{5}-1}\cdot (x-2)`-3\cdot (- (7x^3-x^2-4)^{-2})\cdot (7x^3-x^2-4)`[/m]
[m]y`=\frac{6}{5}\cdot (x-2)^{\frac{1}{5}}+ \frac{3}{(7x^3-x^2-4)^2}\cdot (21x^2-2x)[/m]