Задача 698 На рисунке показан процесс изменения...
Условие
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться. 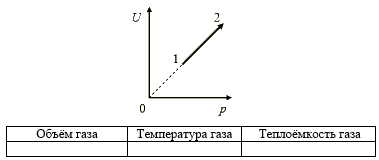
Решение
Ответ: 313
Все решения
2) Т. к.  для идеального газа связано с температурой линейно, то зависимость  от  линейна, следовательно,  Сравнивая полученное выражение с уравнением Менделеева-Клапейрона для одного моля  получаем, что объём газа не изменился.
3) Теплоёмкость газа определяется выражением  В данном процессе работа газа равна нулю, в результате, теплоёмкость оставалась неизменной.