Задача 69744 Решить дифференциальное...
Условие
y'+sin(x +y)=sin(x-y)
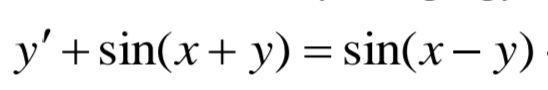
математика ВУЗ
888
Решение
★
[m]y' = 2sin \frac{x-y-x-y}{2} \cdot cos \frac{x-y+x+y}{2}[/m]
[m]y' = 2sin (-y) \cdot cos x[/m]
Получили простое уравнение с разделяющимися переменными
dy/sin y = -2dx/cos x
Интегрируем обе части:
ln |tg(y/2)| = -2ln |tg(x/2 + π/4)| + ln C
ln |tg(y/2)| = ln (tg(x/2 + π/4)^(-2)*C)
tg(y/2) = C/tg^2(x/2 + π/4)
y = 2arctg [C/tg^2(x/2 + π/4)]