Задача 69694 ...
Условие
Дано матричное уравнение
Х⋅⎡⎣⎢−4−5−1−2−1−12−2−2⎤⎦⎥=⎡⎣⎢10117243313⎤⎦⎥
Выясните имеет ли данное уравнение единственное решение. Если решение не существует или оно не единственное, то введите цифру 0 и переходите к следующей задаче.
Если решение единственное, то найдите матрицу Х.
В ответ введите сумму элементов 2-ой строки найденной матрицы Х.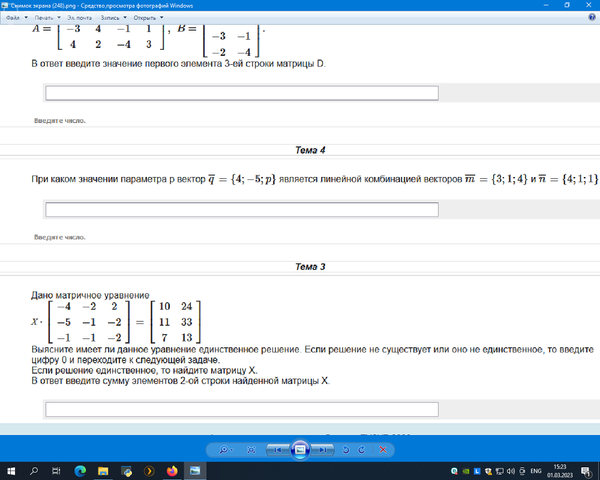
Решение
Значит, матрица X должна быть размером 2х3.
[m]\begin{pmatrix}
X11 & X12 & X13\\
X21 & X22 & X23\\
\end{pmatrix} \cdot \begin{pmatrix}
-4 & -2 & 2 \\
-5 & -1 & -2 \\
-1 & -1 & -2 \\
\end{pmatrix} = \begin{pmatrix}
10 & 24 \\
11 & 33 \\
7 & 13 \\
\end{pmatrix}[/m]
Составляем систему:
{ X11*(-4) + X12*(-5) + X13*(-1) = 10
{ X21*(-4) + X22*(-5) + X23*(-1) = 24
{ X11*(-2) + X12*(-1) + X13*(-1) = 11
{ X21*(-2) + X22*(-1) + X23*(-1) = 33
{ X11*2 + X12*(-2) + X13*(-2) = 7
{ X21*2 + X22*(-2) + X23*(-2) = 13
Разбиваем ее на две системы из 3 уравнений с 3 неизвестными:
1 Система:
{ -4*X11 - 5*X12 - X13 = 10
{ -2*X11 - X12 - X13 = 11
{ 2*X11 - 2*X12 - 2*X13 = 7
3 уравнение делим на -2 и меняем порядок уравнений:
{ - X11 + X12 + X13 = -3,5
{ -2*X11 - X12 - X13 = 11
{ -4*X11 - 5*X12 - X13 = 10
Складываем 1 и 2 уравнения:
-3*X11 = 7,5; X11 = 7,5/(-3); [b]X11 = -2,5[/b]
Подставляем во 2 и 3 уравнения:
{ 5 - X12 - X13 = 11
{ 10 - 5*X12 - X13 = 10
Из 3 уравнения X13 = -5*X12, подставляем во 2 уравнение:
-X12 + 5*X12 = 11 - 5
4*X12 = 6; [b]X12 = 6/4 = 1,5[/b]
X13 = -5*X12 = -5*1,5; [b]X13 = -7,5[/b]
2 Система:
{ -4*X21 - 5*X22 - X23 = 24
{ -2*X21 - X22 - X23 = 33
{ 2*X21 - 2*X22 - 2*X23 = 13
Решается точно также, решите её сами.