Задача 69669 При каком значении параметра р ранг...

63f257933348577249b52495

28.02.2023 17:07:34

При каком значении параметра р ранг матрицы А равен двум?

626fab9a354ab65fb2f43abb

28.02.2023 18:22:53

★

Матрица:
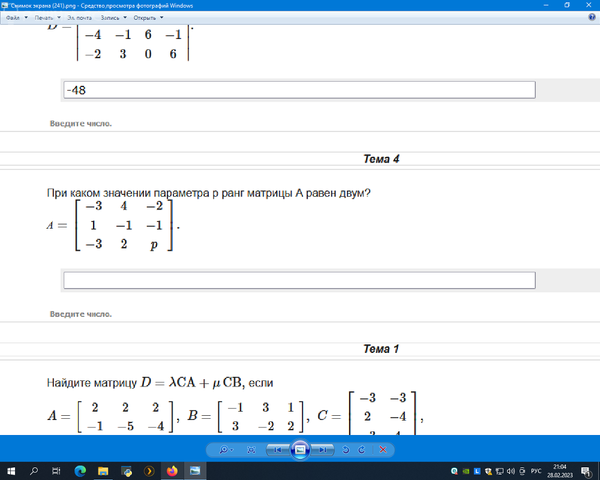
-3 4 -2
1 -1 -1
-3 2 p
Ранг этой матрицы будет равен 2 при условиях:
1) Определитель всей матрицы равен 0.
2) Определитель минора 2 порядка не равен 0.
Найдем определитель следующего минора:
| -3 4 |
| 1 -1 | = (-3)(-1) - 1*4 = 3 - 4 = -1 ≠ 0
Подходит.
Теперь нужно найти такое p, чтобы определитель матрицы был равен 0:
|A| = (-3)(-1)*p + 1*2(-2) + 4(-1)(-3) -
- (-3)(-1)(-2) - 1*4*p - 2(-1)(-3) = 3p-4+12+6-4p-6 = 0
-p + 8 = 0
p = 8