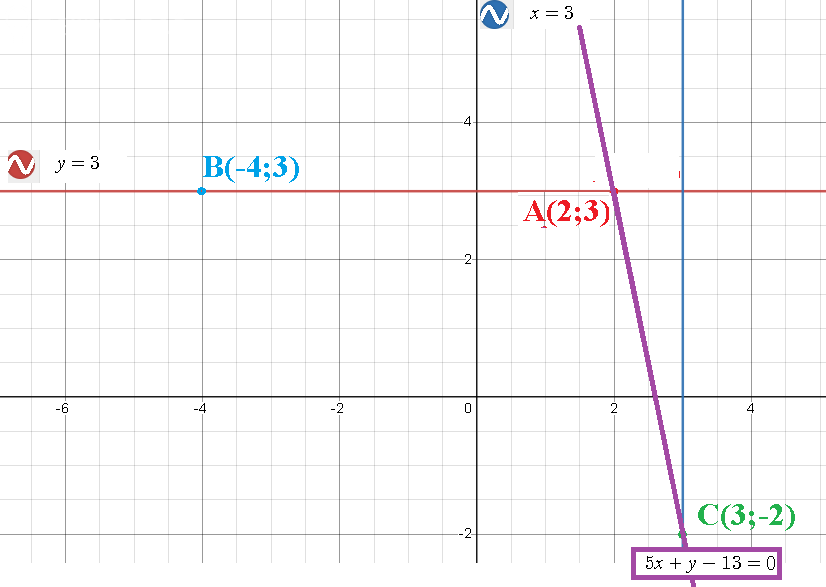
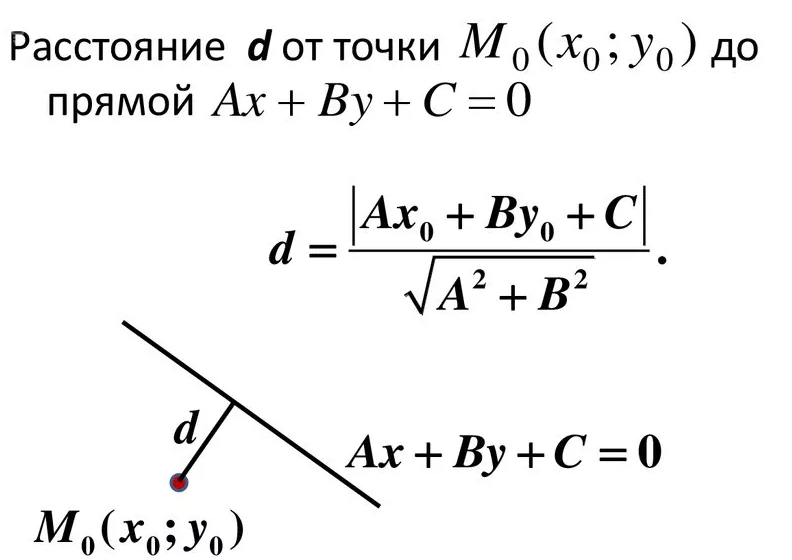Задача 69660 Даны точки А (2;3), В (-4; 3), С (3;...
Условие
А) Найдите длину медианы, проведенной из вершины А треугольника АВС.Б) Составьте общее уравнение прямой АС.
В) Составьте уравнение прямой АВ с угловым коэффициентом.
Г) Составьте уравнение прямой, содержащей высоту СD треугольника АВС.
2.Найдите координаты точки, принадлежащей оси абсцисс и равноудалённой от точек А(-4;2)
и В(3;-4).
3.Составьте уравнение прямой, которая параллельна прямой у= 5х+10 и проходит через центр
окружности х
2
- 2х +у
2−8 у+8=0.
Решение
пусть M(x;0) - точка на оси абсцисс
АМ=ВМ
АМ^2=(x-(-4))^2+(0-2)^2
BM^2=(x-3)^2+(0-(-4))^2
(x-(-4))^2+(0-2)^2=(x-3)^2+(0-(-4))^2
x=
3.
Уравнение прямой:
y=5x-1
как общее уравнение можно записать: 5x-y-1=0
Находим каноническое уравнение окружности:
выделяем полные квадраты
x^2-2x+y^2-8y+8=0
(x^2-2x+1)+(y^2-8y+16)-1-16+8=0
(x-1)^2+(y-4)^2=9 - каноническое уравнение окружности с центром в точке (1;4) R=3
[m]d=\frac{5\cdot 1-4-1|}{\sqrt{5^2+(-1)^2}}=0[/m] ( подставили найденные значения в формулу) см. скрин.
d=0
центр окружности лежит на прямой
1.
A)
M- середина ВС
M(-1/2; 1/2)
AM=sqrt((-1/2)-2)^2+((1/2)-3)^2)=sqrt(-5/2)^2+(-5/2)^2)=(5/2)sqrt(2)
Б)
Общее уравнение прямой:
ax+by+c=0
Подставляем координаты точек A(2;3) и С (3;-2) в общее уравнение прямой
{2a+3b+c=0
{3a-2b+c=0
Вычитаем из первого уравнения второе
-a+5b=0
a=5b
c=-2a-3b=-2*5b-3b=-13b
(5b)*x+by-13b=0
Делим на b
5x+y-13=0 - уравнение прямой АС
В)
Уравнение АB как прямой, проходящей через две точки:
А (2;3)
B(-4;3)
Подставляем координаты точек в уравнение прямой с угловым коэффициентом:
y=kx+b
Решаем систему уравнений:
{3=2k+b
{3=-4k+b
2k+b=-4k+b
6k=0
k=0
3=2k+b ⇒ 3=2*0+b
b=3
y=0x+3 - уравнение прямой АВ как прямой с угловым коэффициентом:
Г)
Высота СD - прямая, перпендикулярная АВ и проходящая через точку С
x=3 - уравнение высоты СD